Osebne zbirke


Podatki, pridobljeni v posmezni raziskavi, so največkrat neurejeni in nepregledni, zato jih moramo urediti oz. narediti pregledne. To storimo na naslednja načina:
če je podatkov malo, jih uredimo po velikosti;
če je podatkov veliko, jih združimo v skupine.
Kako ravnati z njimi, je precej odvisno od samih podatkov. Ločimo:
zvezne podatke;
diskretne podatke.
Zvezni podatki (navadno fizikalne veličine), so tisti podatki, ki lahko v danem intervalu zavzamejo poljubno vrednost.
Diskretne podatke dobimo s štetjem.
Pri podatkih v večini primerov pride do tega, da se nekateri podatki ponavljajo. Koliko krat se ta podatek ponovi imenujemo frekvenca, ki ji pogosto rečemo tudi absolutna frekvenca:
Posamezno število diskretnih statističnih enot iste vrednosti imenujemo frekvenca 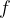 tega statističnega znaka.
tega statističnega znaka.
Če je diskretnih podatkov zelo veliko ali če so podatki zvezni, jih združujemo v skupine ali frekvenčne razrede. Celoten razpon podatkov zajamemo z določenim številom frekvenčnih razredov, ki so ponavadi enako široki, ni pa nujno. Veljata naslednji oznaki:
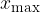 predstavlja podatek z največjo vrednostjo;
predstavlja podatek z največjo vrednostjo;
 predstavlja podatek z najmanjšo vrednostjo;
predstavlja podatek z najmanjšo vrednostjo;
Podatke grupiramo s pomočjo frekvenčnih razredov. Grupiranja se lotimo tako, da podatke razdelimo v frekvenčne razrede. Velikost razreda določimo glede na potrebe konkretnega primera in ga izračunamo na nasednji način:
Širina frekvenčnega razreda 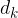 je razlika med zgornjo mejo razreda
je razlika med zgornjo mejo razreda 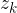 in spodnjo mejo razreda
in spodnjo mejo razreda 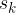 :
:
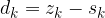
Enako širokim razredom določimo njihovo širino tako, da celoten razpon podatkov 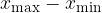 delimo z ustreznim naravnim številom (odvisno od primera).
delimo z ustreznim naravnim številom (odvisno od primera).
Ko enkrat določimo širino frekvenčnega razreda, lahko določimo še sredino posameznega frevenčnega razreda:
Sredina frekvenčnega razreda predstavlja število, ki je srednja vrednost celotnega razreda:
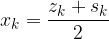
Pri urejanju in analiziranju podatkov moramo biti prav tako pozorni na vrednosti, ki občutno odstopajo. Te vrednosti imenujemo osamelci.
Podatke iz histograma s številkami ponavadi predstavimo še s tabelo, ki ji rečemo frekvenčna porazdelitev. Vsaki vrednosti ali vsaki skupini vrednosti pripišemo število posameznih enot s to vrednostjo ali frekvenco.
Frekvenčna porazdelitev je razvrstitev statističnih enot populacije po vrednosti spremenljivke v pripadajoče razrede. Med tem ko je frekvenca razreda število enot v posameznem razredu. Frekvenco razreda j označimo kot 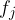 .
.
Zanimive so tudi vrednosti, ki povedo, kolikšen delež celote pomeni posamezna vrednost statističnega znaka oz. število podatkov v frekvenčnem razredu. Kvocient teh dveh števil je relativna frekvenca 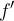 podatka; največkrat ga podajamo v odstotkih:
podatka; največkrat ga podajamo v odstotkih:
Relativna frekvenca razreda 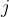 je delež enot populacije, ki je razvrščen v razred
je delež enot populacije, ki je razvrščen v razred 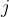 :
:
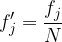
pri čemer je 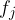 frekvenca razreda j, N pa število podatkov.
frekvenca razreda j, N pa število podatkov.
Poznamo pa še kumulativno frekvenco F, ki pove koliko podatkov je zavzelo manjšo vrednost od zgornje meje frekvenčnega razreda. Poglejmo si kumulativno frekvenco na primeru: