Prijava z e-naslovom
Prijava brez gesla
Stožec je geometrijsko telo, katerega površje je sestavljeno iz okrogle ravne ploskve, nad katero se ovija ukrivljena ploskev. Nasproti okrogle ravne ploskve vedno stoji konica. Ravno ploskev imenujemo osnovna ploskev, konico pa vrh stožca.
Stožce delimo na dve veliki skupini:
pokončne - vrh leži točno nad središčem osnovne ploskve ter
poševne - vrh je zamaknjen od središča osnovne ploskve.
Kot smo videli, poznamo pokončni in poševni stožec, obema pa lahko pripišemo nekaj skupnih lastnosti.
Stožec je okroglo geometrijsko telo, omejeno z eno osnovno ploskvijo in plaščem:
a) osnovna ploskev stožca, b) plašč stožca
Za stožec so značilni naslednji elementi:
Osnovni rob stožca je krožnica, ki omejuje osnovno ploskev.
Os stožca je premica, ki poteka skozi središče osnovne ploskve ter skozi vrh stožca.
Višina stožca je razdalja med ravnino, na kateri se nahaja osnovna ploskev, in vrhom stožca. Višina je daljica, ki je pravokotna na osnovno ploskev.
Stožec nima stranskih robov, saj osnovna ploskev nima oglišč.
Značilni elementi stožca
Stranica stožca je daljica z enim krajiščem na osnovnem robu ter drugim krajiščem v vrhu stožca.
V uvodu smo videli, da razlikujemo pokončne in poševne stožce. Poševni stožci presegajo okvir osnovne šole, zato se bomo bomo v nadaljevanju osredotočili le na pokončne stožce.
V nadaljevanju obravnavamo le pokončne stožce.
Stožec je pokončen, če je njegova os pravokotna na osnovno ploskev. Plašč stožca je v tem primeru krožni izsek. Stranici stožca sta enako dolgi, tako da osni presek predstavlja enakokraki trikotnik.
Za pokončen stožec veljajo naslednje posebnosti:
Plašč pokončnega stožca je krožni izsek.
Višina pokončnega stožca leži na osi stožca.
Stranici pokončnega stožca imata enako dolžino.
Omenjene poenostavitve nam olajšajo računanje površine in prostornine stožca, ki ju bomo spoznali v nadaljevanju.
Površina stožca je seštevek ploščin obeh ploskev, ki omejujeta geometrijsko telo. Mejni ploskvi stožca sta geometrijska lika, katerih ploščini že znamo izračunati. Vsak lik posebej se v celoti nahaja na eni sami ravnini, površina stožca pa je razporejena po več ravninah. Zato mejne ploskve stožca za lažjo predstavo in računanje razgrnemo na ravnino.
Če mejni ploskvi stožca razgrnemo na ravnino, dobimo mrežo stožca. Celotna mreža predstavlja sestavljen geometrijski lik.
Mreža stožca
Mejne ploskve telesa, razgrnjene na ravnino, imenujemo mreža geometrijskega telesa.
Računanje površine stožca si lahko predstavljamo kot računanje ploščine sestavljenega geometrijskega lika. Pri tem najprej izračunamo ploščine posameznih delov lika, nato pa te ploščine seštejemo.
Osnovna ploskev stožca je krog, zato lahko zapišemo:
Ploščina osnovne ploskve stožca O je enaka ploščini kroga, ki predstavlja osnovno ploskev:
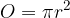
pri čemer je r polmer osnovne ploskve stožca.
Plašč pokončnega stožca ima obliko krožnega izseka. Dolžina krožnega loka v izseku je enaka obsegu osnovne ploskve, polmer pa je enak stranici stožca:
Plašč na mreži pokončnega stožca
Izpeljimo enačbo za ploščino plašča pokončnega stožca.
Enačba za ploščino krožnega izseka na zgornji sliki (označimo ga kar kot plašč) se glasi:
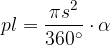
Enačbo hočemo zapisati brez kota kota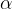 
, zato ga izrazimo s polmerom osnovne ploskve r in stranico stožca s.
Izhajajmo iz naslednjega sorazmerja. Razmerje med kotom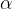 
in polnim kotom je enako razmerju krožnega loka l proti obsegu celotnega kroga o:
Še enkrat zapišimo enačbo za ploščino krožnega izseka:
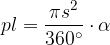
Nadaljujmo z izpeljavo ploščine plašča pokončnega stožca:
Dobili smo enačbo za ploščino plašča pokončnega stožca.
Enačba za ploščino plašča pokončnega stožca pl se glasi:
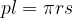
pri čemer je r polmer osnovne ploskve, s pa stranica stožca.
Stožec ima eno samo stransko ploskev, ki je kar enaka njegovemu plašču.
Izpeljimo enačbo za površino pokončnega stožca. Površina stožca je seštevek ploščin osnovne ploskve in plašča:
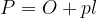
Zapišimo:
Dobili smo enačbo za površino pokončnega stožca.
Enačba za površino pokončnega stožca P se glasi:
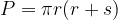
pri čemer je r polmer osnovne ploskve, s pa stranica stožca.
Prostornina pokončnega stožca je velikost prostora, ki ga stožec zavzame.
Splošna enačba za izračun prostornine pokončnega stožca se glasi:
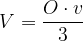
pri čemer je V prostornina stožca, O ploščina osnovne ploskve, v pa višina stožca.
Če v enačbo vstavimo ploščino osnovno ploskve, pa dobimo:
Enačba za izračun prostornine pokončnega stožca V se glasi:
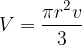
pri čemer je r polmer osnovne ploskve, v pa višina stožca.
Če pokončni stožec prerežemo z ravnino, na kateri leži višina stožca, dobimo enakokraki trikotnik, ki ga imenujemo osni presek stožca:
Osni presek stožca
Osnovnica enakokrakega trikotnika predstavlja premer osnovne ploskve, kraka pa stranici stožca.
Osni presek pokončnega stožca je enakokraki trikotnik.
Osnovnica enakokrakega trikotnika predstavlja premer osnovne ploskve, kraka pa stranici stožca.
Zapišimo enačbo za ploščino osnega preseka pokončnega stožca:
Enačba za izračun ploščine osnega preseka pokončnega stožca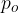 
se glasi:
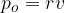
pri čemer je r polmer osnovne ploskve, v pa višina stožca.
Osni presek pokončnega stožca je enakokraki trikotnik. Če ga razpolovimo pravokotno na osnovnico, dobimo dva pravokotna trikotnika:
Pravokotna trikotnika na osnem preseku stožca
Tako za levi kot za desni pravokotni trikotnik lahko zapišemo Pitagorov izrek:
Pri računanju osnega preseka pokončnega stožca uporabimo Pitagorov izrek na pravokotnem trikotniku:
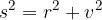
pri čemer je s stranica, r polmer osnovne ploskve, v pa višina stožca.
Stožce razvrščamo glede na različne lastnosti, poznamo pa tudi nekaj posebnih primerov.
Kot smo spoznali že v uvodu, so stožci lahko pokončni ali poševni. Izračuni za poševne stožce presegajo okvir osnovne šole.
To gradivo podrobneje obravnava le pokončni stožec.
Enakostranični stožec ima stranico enako premeru osnovne ploskve:
Enakostranični stožec v poševni projekciji
Površina
Izpeljimo enačbo za površino enakostraničnega stožca.
Izhajamo iz splošne enačbe za površino stožca:
Dobili smo enačbo za površino enakostraničnega stožca.
Enačba za izračun površine enakostraničnega stožca P se glasi:
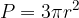
pri čemer je r polmer osnovne ploskve stožca.
Prostornina
Izpeljimo še enačbo za prostornino enakostraničnega stožca s splošno enačbo za prostornino stožca:
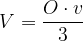
Preden nadaljujemo z izpeljavo, izrazimo višino stožca v s polmerom osnovne ploskve r.
Izhajajmo iz Pitagorovega izreka v pokončnem stožcu:
Nadaljujmo z izpeljavo ploščine plašča pokončnega stožca:
Dobili smo enačbo za prostornino enakostraničnega stožca.
Enačba za izračun prostornine enakostraničnega stožca V se glasi:
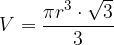
pri čemer je r polmer osnovne ploskve stožca.
Osni presek
Osni presek enakostraničnega stožca je enakostranični trikotnik:
Osni presek enakostraničnega stožca
Osni presek enakostraničnega stožca je enakostranični trikotnik.
Stranica enakostraničnega trikotnika je enaka premeru osnovne ploskve oziroma stranici stožca.
Izpeljimo enačbo za ploščino osnega preseka enakostraničnega stožca.
Izhajamo iz splošne enačbe za ploščino osnega preseka stožca:
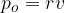
Vanjo bomo vstavili višino, ki smo jo izpeljali višje:
Dobili smo enačbo za ploščino osnega preseka enakostraničnega stožca.
Ploščina osnega preseka enakostraničnega stožca 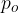se glasi:
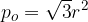
pri čemer je r polmer osnovne ploskve stožca.
