Prijava z e-naslovom
Prijava brez gesla
V gradivu o podobnosti trikotnikov smo povedali, da sta trikotnika podobna, če se ujemata v vseh notranjih kotih.
To znanje uporabimo v naslednjem primeru:
Na podlagi ugotovitev iz zgornjega primera izhajata dva Talesova izreka, ki ju bomo spoznali v nadaljevanju.
Talesova izreka uporabljamo za računanje dolžin v podobnih trikotnikih. Močno nam koristita tudi v resničnem življenju, kjer vseh neznanih dolžin ne moremo enostavno izmeriti z merilom.
Prvi Talesov izrek povezuje razmerja dolžin soležnih odsekov na enem in drugem kraku kota, ki ga sekata vzporednici.
Na zgornji sliki velja enakost razmerij:
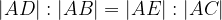
Prvi Talesov izrek se glasi:
Če vzporednici sekata kraka kota, sta dolžini odsekov na enem kraku kota v enakem razmerju kot dolžini istoležnih odsekov na drugem kraku.
Uporabimo ga v primeru.
Drugi Talesov izrek pa povezuje razmerja dolžin soležnih odsekov na enem kraku kota in vzporednicah, ki sekata kot.
Na zgornji sliki velja enakost naslednjih razmerij:
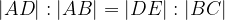
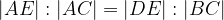
Drugi Talesov izrek se glasi:
Če vzporednici sekata kraka kota, sta dolžini odsekov na enem kraku v enakem razmerju kot dolžini istoležnih odsekov na vzporednicah.
Uporabimo ga v primeru.
