Osebne zbirke


Pri tangentni metodi ničle krivulje iščemo s pomočjo tangent na krivuljo. Ker se tangenta v bližnji okolici dane točke x obnaša podobno kot polinom v dani točki, je tudi njena ničla podobna ničli polinoma.
Iskanje začnemo tako, da izberemo točko, ki se nahaja v bližini ničle. V izbrani točki postavimo tangento na polinom, ter poiščemo ničlo tangente. Dobljena ničla tangente predstavlja naslednji približek ničli. Postopek ponovimo.
Pa poglejmo, kako izpeljemo Newtonovo iteracijsko formulo za iskanje približkov ničel polinoma. Pomagajmo si s skico:
Na sliki imamo polinom p(x) in tangento na dani polinom v točki 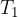 . Zapišimo smerni koeficient tangente (modra linija):
. Zapišimo smerni koeficient tangente (modra linija):
Za preračunavanje približkov uporabimo navedeno iteracijsko formulo. Če je bila začetna točka izbrana v bližini dejanske ničle, potem opazimo, da dobljeni približki hitro konvergirajo proti ničli.
Splošni zapis (za katerokoli funkcijo) iteracijske enčabe za tangentno metodo je:
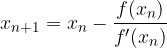
Bližje potencialni ničli, kot si izberemo začetno vrednost x, prej in hitreje se bodo približki približevali pravi ničli.