Osebne zbirke


Trikotnik je geometrijski lik s tremi stranicami in tremi oglišči. Oglišča trikotnika so točke, ki ne ležijo na isti premici.
Na gornji sliki so označeni elementi trikotnika:
oglišča 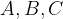 ,
,
stranice 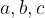 ,
,
notranji koti 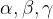 .
.
Trikotnike med seboj razlikujemo po dveh kriterijih:
glede na dolžino stranic in
glede na velikost notranjih kotov.
Poznavanje vrst trikotnikov je ključno pri izračunu obsega, ploščine in velikosti kotov ter pri postopku načrtovanja, kar bomo spoznali v nadaljevanju.
Glede na dolžine stranic trikotnika, ločimo naslednje vrste trikotnikov:
Raznostranični trikotnik
Običajen trikotnik ima stranice različnih velikosti, posledično pa so različne tudi velikosti notranjih kotov. Imenujemo ga raznostranični trikotnik:
Enakokraki trikotnik
Če ima trikotnik dve stranici enako dolgi, ga imenujemo enakokraki trikotnik. Stranici, ki sta enako dolgi, imenujemo kraka trikotnika, tretjo stranico pa osnovnica. V enakokrakem trikotniku sta skladna tudi notranja kota ob osnovnici.
Enakostranični trikotnik
Če ima trikotnik enako dolge vse tri stranice, ga imenujemo enakostranični trikotnik. Tak trikotnik ima enako velike tudi vse notranje kote.
Glede na velikosti notranjih kotov, ločimo naslednje vrste trikotnikov:
Ostrokotni trikotnik
Kadar ima trikotnik vse notranje kote ostre (torej manjše od 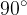 ), ga imenujemo ostrokotni trikotnik.
), ga imenujemo ostrokotni trikotnik.
Pravokotni trikotnik
Kadar je v trikotniku en notranji kot pravi (meri 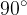 ), tak trikotnik imenujemo pravokotni trikotnik.
), tak trikotnik imenujemo pravokotni trikotnik.
Najdaljšo stranico v pravokotnem trikotniku imenujemo hipotenuza, krajši dve pa kateti. Kateti tvorita pravi kot.
Topokotni trikotnik
Kadar pa je v trikotniku en notranji kot topi (meri več kot 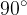 ), potem tak trikotnik imenujemo topokotni trikotnik. Tudi v tem trikotniku sta preostala dva kota ostra.
), potem tak trikotnik imenujemo topokotni trikotnik. Tudi v tem trikotniku sta preostala dva kota ostra.
V trikotniku obravnavamo:
notranje in
zunanje
kote.
Notranji koti
Notranji kot ima vrh v oglišču, njegova kraka pa sta nosilki stranic, ki se stikata v tem oglišču.
V vsakem trikotniku velja, da je vsota notranjih kotov enaka 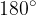 .
.
Zunanji koti
Zunanji kot je sokot pripadajočega notranjega kota. Kota zato ležita v sosednji legi, njuna vsota pa tvori iztegnjeni kot. Tak par kotov ima skupni vrh v oglišču trikotnika.
Zunanji kot najlažje narišemo tako, da eno izmed sosednjih stranic podaljšamo preko oglišča. Poltrak iz podaljšane stranice tvori prvi krak zunanjega kota, drugi krak pa je nosilka druge izmed para sosednjih stranic.
Ker sta notranji in pripadajoči zunanji kot sokota, lahko zapišemo:
Vsota notranjega in pripadajočega zunanjega kota je 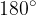 .
.
Za zunanje kote v trikotniku velja tudi:
Vsota zunanjih kotov v trikotniku je 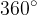 .
.
Višino trikotnika lahko opišemo na dva načina:
kot daljico, ki poteka pravokotno od (nosilke) stranice do nasprotnega oglišča,
oziroma kot razdaljo med nosilko stranice in vzporednico skozi nasprotno oglišče.
Drugi opis je nam pride prav pri načrtovanju trikotnikov s podano višino.
Stranica je daljica, nasproti ležeče oglišče pa je točka. Kot vemo, razdaljo med točko in daljico (oziroma njeno nosilko) merimo pravokotno na daljico, zato je tudi višina vedno pravokotna na stranico.
V praksi višino običajno narišemo od nosilke stranice do oglišča, ki stoji nasproti stranice.
Ker ima trikotnik tri stranice, ima tudi tri višine.
Kot vidimo, v ostrokotnem trikotniku lahko vse tri višine narišemo znotraj trikotnika.
Nosilke vseh treh višin se sekajo v točki, ki jo imenujemo višinska točka. V ostrokotnem trikotniku ta točka leži znotraj trikotnika.
Višinsko točko lahko določimo že z dvema nosilkama višin, tretjo vrišemo zgolj za kontrolo.
Tako kot vsem geometrijskim likom tudi trikotniku lahko določimo najbolj značilni količini, obseg in ploščino:
Pri obsegu se ukvarjamo z merjenjem dolžine sklenjene črte, ki omejuje trikotnik.
Pri ploščini pa z določanjem velikosti dela ravnine znotraj te sklenjene črte.
Obseg merimo v dolžinskih merskih enotah. Osnovna merska enota za dolžino je meter.
Ploščino merimo v ploščinskih merskih enotah. Osnovna merska enota za ploščino je kvadratni meter.
Obseg trikotnika predstavlja dolžino sklenjene lomljene črte, ki omejuje trikotnik.
Obseg izračunamo tako, da seštejemo dolžine vseh stranic trikotnika:
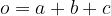
Za posebne trikotnike lahko zgornjo enačbo poenostavimo:
enakokraki trikotnik:
V enakokrakem trikotniku izračunamo obseg s formulo:
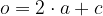
enakostranični trikotnik:
V enakostraničnem trikotniku izračunamo obseg s formulo:
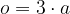
Formula za obseg je vedno vezana na sliko oziroma oznake oglišč in stranic. Ob različni označitvi oglišč se lahko formula razlikuje.
Ploščina trikotnika predstavlja velikost dela ravnine, ki ga omejuje sklenjena lomljena črta, sestavljena iz njegovih stranic.
Izračunamo jo po naslednjem obrazcu.
Enačba za ploščino trikotnika se glasi:
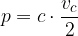
pri čemer je c poljubna stranica trikotnika, 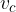 pa višina na to stranico.
pa višina na to stranico.
Gornjo enačbo za izračun ploščine lahko izpeljemo tako, da trikotnik preoblikujemo v pravokotnik.
Trikotnik lahko poljubno zasukamo. Zato lahko njegovo ploščino izračunamo s katerokoli stranico in višino na to stranico:
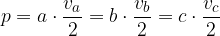
Ploščino v pravokotnem trikotniku izračunamo s formulo:
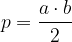
Trikotnik lahko narišemo le, če je skupna dolžina dveh njegovih stranic večja od dolžine tretje stranice. To pravi pravilo trikotniške neenakosti.
Trikotniška neenakost pravi, da je vsota poljubnih dveh stranic trikotnika večja od tretje:
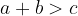
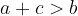
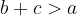
Če velja ena od gornjih neenačb, potem veljata tudi drugi dve. Zato je za trikotniško neenakost dovolj zapisati eno neenačbo.
Poglejmo še, kdaj s tremi stranicami trikotnika ni mogoče sestaviti.
Če imamo na voljo tri stranice, za katere ne velja trikotniška neenakost, potem z njimi ne moremo sestaviti trikotnika. To se zgodi, če je poljubna stranica predolga - daljša ali enaka kot vsota drugih dveh stranic. Zapišimo primer, ko je stranica  daljša od vsote stranic
daljša od vsote stranic 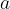 in
in 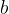 . Povedano drugače - vsota stranic
. Povedano drugače - vsota stranic 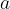 in
in 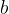 je krajša ali enaka od stranice
je krajša ali enaka od stranice  :
:
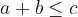
Če na lepenko narišemo trikotnik in ga v ležečem položaju postavimo na konico prsta, potem moramo trikotnik s prstom podpreti v točno določeni točki, da se ne prevesi in pade na tla. Takšna točka je samo ena in jo imenujemo težišče.
Težišče na splošno lahko določimo kateremu koli liku ali telesu. Težišče trikotnika pa določimo s pomočjo težiščnic. Težiščnica trikotnika je daljica, ki poteka od razpolovišča stranice do nasprotnega oglišča.
V trikotniku so tri težiščnice, za vsako stranico po ena:
težiščnica na stranico 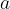 , označimo jo s
, označimo jo s 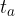 ,
,
težiščnica na stranico 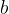 , označimo jo s
, označimo jo s 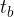 ,
,
težiščnica na stranico  , označimo jo s
, označimo jo s 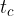 .
.
Presečišče težiščnic imenujemo težišče. Običajno ga označimo s točko 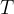 . Za določanje težišča zadoščata že dve težiščnici, tretja je zgolj za kontrolo.
. Za določanje težišča zadoščata že dve težiščnici, tretja je zgolj za kontrolo.
Točko, v kateri moramo podpreti trikotnik, da se bo obdržal v ravnovesni legi, imenujemo težišče. To je točka, v kateri se sekajo težiščnice trikotnika.