Prijava z e-naslovom
Prijava brez gesla
Vsakemu trikotniku lahko včrtamo in očrtamo krožnico.
Včrtana krožnica se, kot že ime pove, nahaja znotraj trikotnika. Omejena je s stranicami trikotnika in se dotika vseh treh stranic trikotnika. Njeno središče označimo z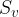 
.
Očrtana krožnica pa poteka "okoli" trikotnika, vpeta je namreč na njegova oglišča. Očrtana krožnica poteka skozi vsa oglišča trikotnika. Njeno središče označimo z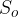 
.
Včrtana krožnica - modra; očrtana krožnica - rdeča
Včrtana krožnica se dotika vseh stranic trikotnika. To pomeni, da je:
njeno središče enako oddaljeno od nosilk vseh treh stranic,
njen polmer pa enak razdalji med središčem in nosilko poljubne stranice.
Poglejmo, kako določimo središče in polmer trikotniku včrtane krožnice. Najti moramo točko, ki je enako oddaljena od vseh stranic, oziroma povedano pravilno, enako oddaljena od vseh treh nosilk stranic.
Vemo, da simetrala kota predstavlja množico točk, ki so enako oddaljene od krakov kota. Točke na simetrali posameznega notranjega kota trikotnika so torej enako oddaljene od obeh krakov, ki se stikata v vrhu tega kota.
Simetrale vseh treh notranjih kotov trikotnika se stikajo v točki, ki je enako oddaljena od vseh treh nosilk stranic trikotnika. To pa je središče trikotniku včrtanega kroga.
Tako v ostrokotnem kot v topokotnem trikotniku se središče trikotniku včrtanega kroga nahaja v notranjosti trikotnika:
Ostrokotnemu trikotniku včrtana krožnica
Topokotnemu trikotniku včrtana krožnica
Potek načrtovanja včrtane krožnice si oglejmo na naslednjem primeru.
Očrtana krožnica poteka skozi vsa oglišča trikotnika, kar pomeni, da je:
njeno središče enako oddaljeno od vseh treh oglišč,
njen polmer pa enak razdalji med središčem in poljubnim ogliščem.
Da določimo, kje leži središče trikotniku očrtane krožnice, moramo najti točko, ki je enako oddaljena od vseh treh oglišč trikotnika.
Vemo, da simetrala daljice predstavlja množico točk, ki so enako oddaljena od krajišč daljice. Vsaka stranica trikotnika je tudi daljica, zato lahko narišemo simetralo vsake stranice. Krajišča stranic so oglišča trikotnika.
Točke na simetrali posamezne stranice so torej enako oddaljene od obeh oglišč. Simetrale vseh treh stranic trikotnika se stikajo v eni točki, ki je enako oddaljena od vseh treh oglišč trikotnika. To pa je središče trikotniku očrtanega kroga.
V ostrokotnem trikotniku se središče včrtane krožnice nahaja v notranjosti trikotnika:
Ostrokotnemu trikotniku očrtana krožnica
V topokotnem trikotniku pa je središče očrtane krožnice zunaj trikotnika:
Topokotnemu trikotniku očrtana krožnica
Potek načrtovanja včrtane krožnice si oglejmo na naslednjem primeru.
