Osebne zbirke


Ulomek v matematiki predstavlja racionalni število in ga zapišemo v naslednji obliki:
pri čemer sta a in b celi števili in je b različen od nič.
Opomba: v literaturi zaznamo tudi ulomek zapisan kot: 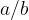
Imenovalec v ulomku nam pove na koliko enakih delov razdelimo celoto, števec pa število delov, ki jih vzamemo.
Poglejmo si še grafični primer ulomka:
Prav tako, lahko vsako racionalno število zapišemo kot ulomek:
Poglejmo si ulomke s stališča celote:
Imenovalec je enak nič
Vemo, da celote ne moremo razdeliti na 0 enakih delov, zato ulomek 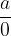 nima pomena. Iz tega sledi zgornja predpostavka, da mora biti imenovalec različen od nič.
nima pomena. Iz tega sledi zgornja predpostavka, da mora biti imenovalec različen od nič.
Imenovalec je enak ena
Če celoto pustimo pomeni, da smo jo razdelili na 1 del. Torej je celota ostala enaka in iz tega sledi sklep:
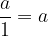
Števec je enak nič
Opazimo, da je v tem primeru števec enak nič. To pomeni, da 0 razdelimo na b delov. Torej je vsak del enak 0 in iz tega sledi :
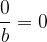
Opomba: Upoštevati moramo predpostavko, da je imenovalec različen od 0.
V nadaljevanju si bomo zgoraj navedena pojma pogledali ločeno:
Ulomka 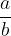 in
in 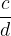 sta enaka oziroma ekvivalentna natanko takrat, ko je
sta enaka oziroma ekvivalentna natanko takrat, ko je 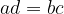 . Torej:
. Torej:
Za enaka ulomka velja:
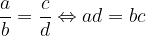
Enaka ulomka sta različna zapisa za isto racionalno število.
Množico vseh racionalnih števil označimo s črko 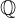 . Racionalna število je število, ki ga lahko izrazimo kot količnik (kvocient) dveh celih števil. To imenujemo ulomki. Vemo, da lahko poljubno celo število zapišemo kot ulomek z imenovalcem 1, torej so racionalna števila
. Racionalna število je število, ki ga lahko izrazimo kot količnik (kvocient) dveh celih števil. To imenujemo ulomki. Vemo, da lahko poljubno celo število zapišemo kot ulomek z imenovalcem 1, torej so racionalna števila  razširitev množice celih števil
razširitev množice celih števil  .
.
Matematično to zapišemo kot:
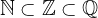
Racionalna števila ponazarjamo na številski premici. Vsakemu racionalnemu številu pripada na številski premici natanko določena točka.
Ulomek, pri katerem je števec večji od imenovalca, je vedno večji od 1, saj to pomeni, da smo vzeli več delov, kot smo jih dobili pri delitvi celote.
Nasprotni ulomek ulomka 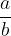 je ulomek
je ulomek 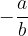 . Vsota danega in njemu nasprotnega mora biti enaka nič:
. Vsota danega in njemu nasprotnega mora biti enaka nič:
Vsota ulomka in pripadajočega nasprotnega ulomka:
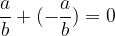
Opomba: nasprotni ulomek nasprotnega ulomka je enak danemu ulomku:
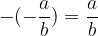
Množica racionalnih števil je urejena. Za ulomka 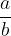 in
in 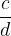 velja natanko ena od naslednjih treh možnosti:
velja natanko ena od naslednjih treh možnosti:
Prvi ulomek je večji od drugega:
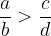
Prvi ulomek je manjši od drugega:
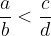
Ulomka sta enaka:
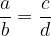
Za relaciji biti manjši in biti večji veljajo naslednje lastnosti:
Če na obeh straneh neenakosti prištejemo isto število, se neenakost ohrani (monotonost vsote). Če velja:
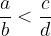
potem velja tudi:
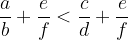
Relacija je tranzitivna. Če veljata zvezi:
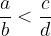
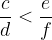
potem velja tudi:
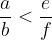
Pri množenju neenakosti s pozitivnim številom se znak neenakosti ohranja. Če velja
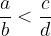
kjer je
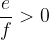
potem velja tudi
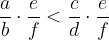
Pri množenju neenakosti z negativnim številom se znak neenakosti obrne. Če velja:
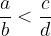
kjer je
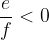
potem velja:
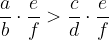
Poudarimo to točko: pri prehodu na nasprotno vrednost se neenačaj obrne. Torej, če je
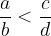
potem sledi, da je
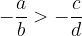
Vsako racionalno število lahko ponazorimo kot točko na številski premici. Slika večjega racionalnega števila je na številski premici desno od slike manjšega racionalnega števila.
Slike slike negativnih števil ležijo levo od koordinatnega izhodišča, slike pozitivnih racionalnih števil pa desno.
Ker sta števec ali imenovalec lahko tudi negativna, si poglejmo, kako predznak v števcu ali imenovalcu vpliva na predznak celotnega ulomka  .
.
Negativni števec
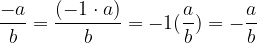
Negativni imenovalec
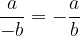
Negativni števec in negativni imenovalec:
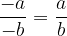
S pomočjo teh trditev lahko podamo sklep:
Če imata števec in imenovalec različen predznak je ulomek negativen, sicer je pozitiven.