Osebne zbirke


V tem poglavju bomo navedli nekaj primerov najpogostejše rabe eksponentne in logaritemske funkcije v praksi.
V praksi se pojavljajo primeri, kjer neka količina eksponentno pada in primeri, kjer neka količina eksponentno narašča, zato bomo ločili:
eksponentno rast
eksponentno padanje
Če se neka količina (denar, prebivalstvo ...) v enakih časovnih intervalih povečuje s konstantnim faktorjem, tako rast imenujemo eksponentna rast.
V vsakdanjem življenju se zelo pogosto srečamo s primeri, kot je naslednji.
Z eksponentno funkcijo lahko opišemo tudi rast prebivalstva, če vemo začetno število prebivalstva, ki jo označimo z 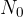 , prirastek, ki ga označimo s k in število let za katero računamo spremembo, ki ga označimo s t.
, prirastek, ki ga označimo s k in število let za katero računamo spremembo, ki ga označimo s t.
Funkcijo potem lahko zapišemo kot:
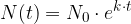
Kadar se neka količina (količina radioaktivnega elementa, spomin ... ) v enakih časovnih intervalih zmanjšuje s konstantnim faktorjem govorimo o eksponentnem padanju, ki ga opišemo z eksponentno funkcijo.
Zmanjševanje števila jeder radioaktivnega elementa pa opišemo z enačbo:
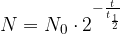
kjer, je  število jeder na začetku,
število jeder na začetku, 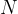 število jeder po času t,
število jeder po času t, 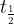 pa čas, v katerem se število jeder zmanjša na polovico začetne vrednosti.
pa čas, v katerem se število jeder zmanjša na polovico začetne vrednosti.
Starost organizma določajo z ugotavljanjem razpada radioaktivnega izotopa 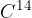 , ki se nahaja v tkivih živih organizmov. Ta s smrtjo organizma začne eksponentno razpadati:
, ki se nahaja v tkivih živih organizmov. Ta s smrtjo organizma začne eksponentno razpadati:
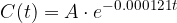
kjer je t čas razpada, A pa začetna količina ogljika v organizmu.
Richterjeva lestvica za merjenje jakost potresnih sunkov je predstavljena v spodnji tabeli:
Richterjeva lestvica je podana z logaritemsko funkcijo:
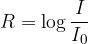
kjer je 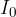 jakost komaj zaznavnega potresa in
jakost komaj zaznavnega potresa in 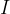 jakost potresa, ki jo zazna seizmogram in jo izražamo z
jakost potresa, ki jo zazna seizmogram in jo izražamo z 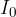 .
.
Občutljivost ušesa za zvok je približno logaritemsko odvisna od jakosti zvoka, zato je glasnost zvoka (G) v decibelih podana z enačbo:
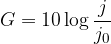
kjer je 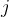 jakost zvoka in
jakost zvoka in 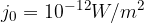 jakost zvoka, ki ga še komaj slišimo oziroma meja slišnosti.
jakost zvoka, ki ga še komaj slišimo oziroma meja slišnosti.
Vrednosti glasnosti zvoka v dB so predstavljene na spodnji tabeli:
Z merjenje kislosti oziroma bazičnosti v kemiji uporabljamo pH vrednost, ki jo izračunamo kot negativni desetiški logaritem oksonijevih ionov:
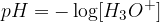
V praksi moramo velikokrat množici točk v koordinatnem sistemu prirediti graf, ki se točkam najbolje prilega. Veliko lažje je množici točk v koordinatnem sistemu prirediti premico, kot pa na primer eksponentno krivuljo. Ker pa to v koordinatnem sistemu z linearnima skalama vedno ni mogoče, namesto linearne skale, uporabljamo logaritemsko skalo.
Logaritemsko skalo navadno uporabimo na ordinatni osi, na abscisni osi pa linearno merilo. Koordinatni sistem z opisanima skalama imenujemo logaritemski papir.
Kaj se z eksponentno funkcijo zgodi na logaritemskem papirju, si oglejmo na spodnjem primeru.
Opazimo, da je graf eksponentne funkcije na logaritemskem papirju premica. Ko na logaritemski papir vnašamo vrednosti za y, se te vrednosti logaritmirajo.
Poglejmo, kaj se na logaritemskem papirju zgodi še matematično. Naj ima naša eksponentna funkcija enačbo:
Dobljena enačba predstavlja enačbo premice, s smernim koeficientom 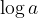 in začetno vrednostjo
in začetno vrednostjo 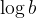 , zato je graf eksponentne funkcije na logaritemskem papirju premica.
, zato je graf eksponentne funkcije na logaritemskem papirju premica.