Osebne zbirke


Matematični izraz (imenujemo ga tudi algebrski izraz) je zapis, ki je lahko sestavljen iz števil ali spremenljivk, ki predstavljajo števila in jih označujemo z majhnimi tiskanimi črkami.
Med izrazi potekajo računske operacije in funkcije, ki jih povezujejo, z oklepaji pa določimo vrstni red računanja.
pri čemer je zapis 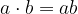 . Znak za množenje lahko tudi izpustimo.
. Znak za množenje lahko tudi izpustimo.
Kadar izraz pomnožimo s poljubnim številom n oz. spremenljivko a, dobimo n-ti oz. a-ti večkratnik tega izraza.
Število b je večkratnik števila a, če ga lahko zapišemo kot:
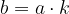
pri čemer je k poljubno naravno (oziroma celo) število.
Večkratnike števila a dobimo tako, da število a zapored pomnožimo z naravnimi (celimi) števili:
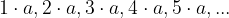
Množico vseh večkratnikov števila a označimo z 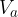 :
:
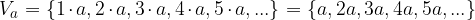
Vsak od nas je že kdaj razstavil kakšno stvar na delčke, ki jih ni bilo mogoče razstaviti na manjše; taka vrsta razstavljanja se v matematiki imenuje razstavljanje na prafaktorje. Razstaviti izraz pomeni zapisati izraz kot produkt faktorjev, ki jih ne moremo razcepiti.
Vsako naravno število lahko na en sam način razcepimo na prafaktorje (praštevila) oziroma zapišemo kot produkt potenc s praštevilskimi osnovami:
Razcep naravnega števila n na prafaktorje (praštevila):
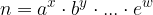
kjer so 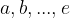 praštevila;
praštevila; 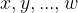 pa eksponenti, ki so naravna števila.
pa eksponenti, ki so naravna števila.
Z izrazi računamo tako, da najprej odpravimo oklepaje, pri čemer upoštevamo vrstni red računskih operacij. in sicer ima množenje prednost pred seštevanjem in odštevanjem, posebej pozorni pa moramo biti na predznake pred oklepaji, saj če imamo pred oklepajem minus, vsi členi v oklepaju spremenijo predznake. Pri razstavljanju in razčlenjevanju izrazov si pomagamo z določenimi formulami.
Kvadrat vsote dvočlenika:
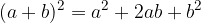
pri čemer dvočlenik pomeni izraz v katerem nastopata dva člena.
Kvadrat razlike dvočlenika:

pri čemer dvočlenik pomeni izraz v katerem nastopata dva člena.
Kub vsote dvočlenika:
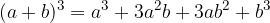
pri čemer dvočlenik pomeni izraz v katerem nastopata dva člena.
Kub razlike dvočlenika:
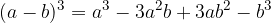
pri čemer dvočlenik pomeni izraz v katerem nastopata dva člena.
Razlika kvadratov dvočlenika:
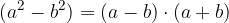
pri čemer dvočlenik pomeni izraz v katerem nastopata dva člena.
Razlika kubov dvočlenika:
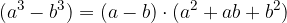
pri čemer dvočlenik pomeni izraz v katerem nastopata dva člena.
Vsota kubov dvočlenika:
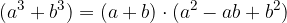
pri čemer dvočlenik pomeni izraz v katerem nastopata dva člena.
Razcep razlike n-tih potenc:
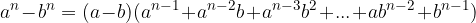
pri čemer je n naravno število.
Razcep kvadratnega tričlenika:
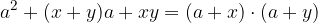
pri čemer tričlenik pomeni izraz v katerem nastopajo trije členi.
Izpostaviti skupni faktor pomeni, da pred oklepaj zapišemo največ, kar imajo vsi členi skupnega. Kar nam od posameznih členov ostane, pa zapišemo v oklepaj.
Pri izpostavljanju je vedno dobro narediti še preizkus in sicer tako, da z izpostavljenim faktorjem pomnožimo izraz v oklepaju in če dobimo začetni izraz, smo pravilno izpostavili.
Sedaj si poglejmo še primer v katerem zraven neznank nastopajo tudi števila.