Osebne zbirke


V prostoru si izberimo dve poljubni točki A in B, ki ju povežemo z daljico, ki jo usmerimo od A proti B ali od B proti A. Dobljeno usmerjeno daljico imenujemo vektor.
Vektorje označujemo tako, da dvema krajnima točkama nadpišemo puščico:
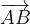
ali zaradi lažjega zapisa kar z malimi črkami:
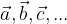
kjer natančno razložimo katere usmerjene daljice predstavljajo ti vektorji.
Vsak vektor je določen z
velikostjo,
usmerjenostjo,
smerjo.
Poglejmo si vse tri pojme podrobneje.
Velikost (imenujemo jo tudi absolutna vrednost) vektorja predstavlja dolžina daljice od začetne do končne točke, njegova smer pa je podana z njegovo lego v prostoru.
Oznaka velikosti vektorja 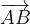 :
:
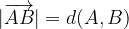
V nalogah bomo uporabljali prvi zapis (absolutno vrednost) za dolžino vektorja.
Smer vektorja, je določena s premico nosilko na kateri je vektor.
Usmerjenost vektorja določa vrstni red začetne in končne točke na premici nosilki. Usmerjenost prikažemo s smerjo puščice nad točkama.
Glede na usmerjenost, ločimo enake in nasprotne vektorje.
Vektorja sta enaka, če sta:
enako dolga
vzporedna
enako usmerjena
Vsak vektor leži na premici, ki jo imenujemo nosilka vektorja. Vektor se ne spremeni, če ga premikamo gor in dol po nosilki ali premici vzporedni nosilki, dokler mu ne spremenimo smeri ali velikosti.
Če zamenjamo začetno (A) in končno točko (B) vektorja 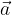 , dobimo nov vektor, ki ima nasprotno smer od prvotnega. Dobljeni vektor označimo z
, dobimo nov vektor, ki ima nasprotno smer od prvotnega. Dobljeni vektor označimo z 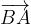 ali z
ali z 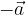 .
.
Vektorja sta nasprotna, če sta:
enako dolga
vzporedna
nasprotno usmerjena
Krajevne vektorje običajno rišemo v koordinatnem sistemu in sicer je krajevni vektor vektor, ki sega od izhodišča koordinatnega sistema do izbrane točke v prostoru. Krajevni vektor točke A, označimo z 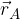 in ima enake koordinate kot točka A.
in ima enake koordinate kot točka A.
Kot bomo videli kasneje, imajo krajevni vektorji velik pomen pri računskih operacijah, saj v praksi z njimi povsod operiramo.
Krajevni vektor 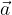 je enolično določen s komponentami.
je enolično določen s komponentami.
V ravnini (dvodimenzionalnem prostoru) ga določajo dve koordinati:
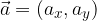
v tridimenzionalnem prostoru pa tri koordinate:
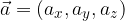
Vektor nič ali ničelni vektor (oznaka 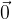 ) ima dolžino nič, nima pa definirane smeri in usmerjenosti.
) ima dolžino nič, nima pa definirane smeri in usmerjenosti.
Enotski vektorji so vektorji z dolžino ena.