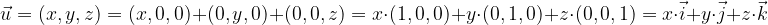Osebne zbirke
Prijava z e-naslovom
Prijava brez gesla
Poljuben vektor v ravnini (prostoru) lahko na en sam način izrazimo kot linearno kombinacijo baznih vektorjev v ravnini (prostoru), pri čemer
bazo ravnine sestavljata dva poljubna neničelna in nevzporedna vektorja (ravnina je dvodimenzionalen prostor)
bazo prostora pa trije poljubni neničelni in nevzporedni vektorji (prostor je trodimenzionalen prostor).
Če vektorje rišemo v pravokotni koordinatni sistem v ravnini, bazna vektorja označimo z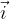 
in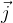 
kot kaže Slika1.
Slika1
Če je pravokotni koordinatni sistem podan v prostoru, bazne vektorje označimo z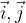 
in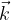 
kot kaže Slika2.
Slika2
Za bazne vektorje v ravnini in prostoru veljajo naslednje lastnosti:
so dolžine 1 enota (so enotski vektorji)
so paroma pravokotni
vektor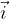 
ima enako smer kot os x, vektor 
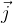ima enako smer kot os y in vektor 
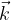ima enako smer kot os z, kot kažeta Slika1 in Sika2.
Bazo ravnine imenujemo standardna ortonormirana baza ravnine, ki jo sestavljata dva bazba vektorja 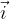in 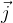z naslednjimi komponentami:
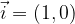
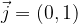
Podobno bazo prostora imenujemo standardna ortonormirana baza prostora, sestavljajo pa jo trije bazni vektorji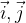 
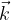in z naslednjimi komponentami:
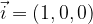
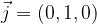
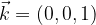
Vektorje v pravokotni koordinatni sistem v ravnini (ali prostoru) običajno rišemo tako, da za začetno točko izberemo kar izhodišče koordinatnega sistema. Takšne vektorje imenujemo krajevni vektorji.
Krajevni vektor točke A je vektor z začetno točko v koordinatnem izhodišču, njegova končna točka je pa kar točka A. Označimo ga z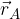 
, njegove komponente pa so enake koordinatam točke A.
Vsa pravila in formule, ki veljajo za vektorje z dvema komponentama, veljajo tudi za vektorje s tremi komponentami, torej za vektorje v pravokotnem koordinatnem sistemu v prostoru.
Vektor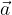 
s komponentama 
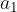in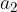 
ter vektor 
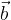s komponentama 
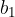in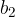 
, seštejemo tako, da seštejemo istoležne komponente.
Vektorja
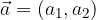
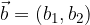
seštejemo tako, da seštejemo njune komponente:
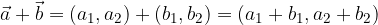
Vektor 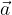s komponentama 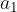in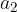 
pomnožimo s številom (skalarjem) tako, da s tem številom (skalarjem) pomnožimo posamezno komponento vektorja.
Vektor
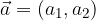
pomnožimo z realnim številom k tako, da z realnim številom k pomnožimo vsako od njegovih komponent:
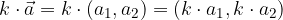
Preden izpeljemo dolžino vektorja, se spomnimo Pitagorovega izreka, ki pravi, da je v pravokotnem trikotniku, kvadrat hipotenuze (c) enak vsoti kvadratov katet (a in b):
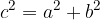
Sedaj v pravokotni koordinatni sistem v ravnini narišimo vektor 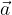z začetno točko v izhodišču, ter komponentama 
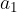in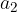 
kot kaže Slika3.
Slika3
Dolžina vektorja 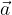je ravno hipotenuza pravokotnega trikotnika, komponenti vektorja 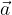pa sta njegovi kateti.
Formula za izračun dolžine vektorja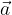 
s komponentama 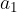in 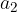, izpeljana iz Pitagorovega izreka, se glasi:
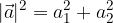
oziroma, če izrazimo dolžino vektorja:
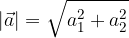
kjer sta 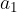prva komponenta vektorja (odsek na osi x), 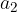pa druga komponenta vektorja (odsek na osi y).
Komponente vektorja s poljubno začetno točko A in poljubno končno točko B dobimo tako, da od krajevnega vektorja končne točke (ki ima komponente enake koordinatam točke B) odštejemo krajevni vektor začetne točke (katerega komponente so enake koordinatam točke A):
Dani sta poljubni točki A in B, ki ju določata krajevna vektorja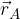 
in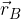 
. Komponente vektorja 
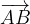izračunamo:
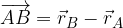
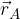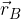Krajevni vektor točke S, ki je razpolovišče daljice AB je enak polovici vsote krajevnih vektorje in (seštejemo krajevna vektorja, ki določata daljico in vsoto delimo z 2).
Če je S razpolovišče daljice AB, potem je krajevni vektor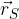 
enak:
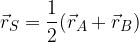
Komponente krajevnega vektorja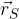 
so hkrati koordinate točke S.
Poljuben vektor
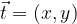
v ravnini lahko izrazimo z baznima vektorjema
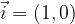
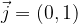
na dva načina:
Poljubni vektor izražen z baznimi vektorji, prvi način
Prvi način je, da prvo komponento vektorja pomnožimo z baznim vektorjem 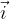, drugo komponento pa z baznim vektorjem 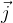, kar pomeni, da vektor 
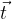s komponentama (x,y) izrazimo kot:
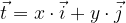
Poljubni vektor izražen z baznimi vektorji, drugi način
Drugi način pa je, da komponente vektorja razčlenimo do komponent baznih vektorjev, kar pomeni, da vektor 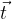s komponentama (x,y) izrazimo kot:
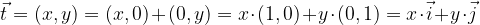
Na podoben način poljuben vektor
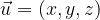
v prostoru lahko izrazimo z baznimi vektorji
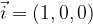
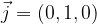
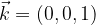
na dva načina:
Poljubni vektor izražen z baznimi vektorji, prvi način
Prvi način je, da prvo komponento vektorja pomnožimo z baznim vektorjem 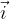, drugo komponento z baznim vektorjem 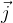in tretjo komponento z baznim vektorjem 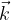, kar pomeni, da vektor 
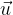s komponentami (x,y,z) izrazimo kot:
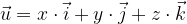
Poljubni vektor izražen z baznimi vektorji, drugi način
Drugi način pa je, da komponente vektorja razčlenimo do komponent baznih vektorjev, kar pomeni, da vektor 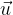s komponentama (x,y,z) izrazimo kot:
