Osebne zbirke


Vzporednost in pravokotnost sta temeljni relaciji med geometrijskimi elementi, tako v ravnini kot tudi v prostoru.
V ravninski geometriji ju najlažje ponazorimo z dvema premicama:
Za vzporedni premici v ravnini obstajata natanko dve možnosti:
imata neskončno skupnih točk (premici sovpadata):
nimata nobene skupne točke:
Vzporedni premici z matematičnimi simboli zapišemo kot
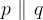
Pravokotni premici pa predstavljata poseben primer presečišča premic; sekata se namreč tako, da oklepata pravi kot (90° v stopinjah oziroma 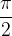 v radianih):
v radianih):
Pravokotni premici z matematičnimi simboli zapišemo kot
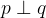
Relacijo pravokotnosti uporabljamo tudi pri določanju razdalje med geometrijskimi elementi ter pri projiciranju:
Razdalja med točko in premico predstavlja najkrajšo razdaljo med njima, to je pravokotno na premico.
Narišimo v ravnini premico p in točko T. Nato skozi točko T potegnimo pravokotnico na premico p. Pravokotnico označimo s q, presečišče med premicama pa s točko A:
Razdalja med točko T in premico p je odsek pravokotnice q med točko T in presečiščem premic p in q.
Z matematičnimi simboli razdaljo med točko T in premico p zapišemo na naslednji način: 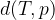
Velja tudi enakost: 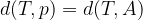
Razdalja med premicama predstavlja najkrajšo razdaljo med njima, to je pravokotno na obe premici.
Enotno razdaljo med premicama lahko določimo le takrat, kadar sta premici vzporedni.
Narišimo v ravnini premici p in q. Nato nanju narišimo pravokotnico r in presečišči označimo z M in N:
Razdalja med premicama p in q je dolžina daljice MN, katere nosilka je pravokotnica na premici p in q in seka ti dve premici v točkah M in N.
Z matematičnimi simboli razdaljo med premicama p in q zapišemo na naslednji način: 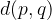
Velja tudi enakost: 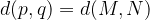
Kot vemo, razdaljo med točko in premico predstavlja najkrajša pot med njima, to je pravokotno na premico. Ob pogledu na naslednjo sliko ugotovimo, da tudi za določanje pravokotne projekcije točke na premico uporabljamo enako metodo:
Pravokotna projekcija točke T na premico p je točka T', ki leži na presečišču premice p in tiste pravokotnice nanjo, ki poteka skozi točko T.
Sedaj, ko znamo na premico projicirati točko, enako lahko storimo tudi z daljico. Ker je daljica ravna črta, lahko projiciramo zgolj njeni krajišči in ju nato povežemo:
Pravokotna projekcija daljice AB na premico p je daljica d', ki leži na premici p, njeni krajišči pa sta pravokotni projekciji krajišč daljice na premico p.