Osebne zbirke
Prijava z e-naslovom
Prijava brez gesla
Funkcije si predstavljamo kot krivulje v ravnini, ki so lahko pretrgane ali nepretrgane. Kadar so nepretrgane, pravimo da je funkcija zvezna, če pa je krivulja v kakšni točki prekinjena, pravimo da je funkcija nezvezna.
Torej, intuitivno si lahko zveznost predstavljamo tako, da če začnemo na papir s svinčnikom risati funkcijo, je ta zagotovo zvezna vse dotlej, dokler svnčnika ne dvignemo stran od papirja.
Funkcija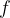 
je v točki 
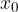zvezna natanko takrat, ko je v točki 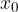definirana in ima limito:
Funkcija ima limito in je zvezna v
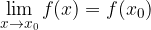
Obrat ne velja. Funkcija v 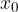ima lahko limito, vendar v 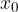ni zvezna.
Funkcija ima limito, ni pa zvezna v
Funkcija 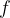je zvezna na intervalu 
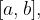če je zvezna v vsaki točki tega intervala.
Če gremo z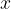 
proti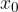 
z leve strani, govorimo o levi limiti.
Oznaka za levo limito: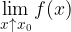 
Število A je leva limita funkcije 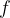v točki 
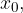če za vsak 
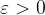obstaja 
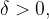da za vsak 
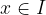iz 
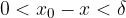sledi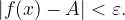 
Oznaka:
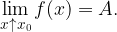
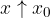pomeni, da 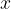narašča k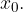 
Zgornjo matematično definicijo najlažje razložimo s pomočjo slike. Torej, poglejmo spodnjo sliko in opazujmo funkcijske vrednosti, ko se z leve približujemo 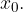Opazimo, da se funkcijske vrednosti približujejo 
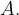Zato je leva limita v točki 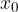enaka
Leva limita: proti x se bližamo z leve strani
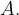
Če gremo z 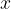proti 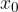z desne strani, govorimo o desni limiti.
Oznaka za desno limito: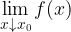 
Število A je desna limita funkcije 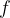v točki 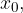če za vsak 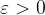obstaja 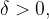da za vsak 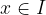iz 
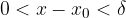sledi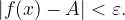
Oznaka:
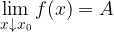
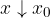pomeni, da 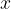pada k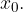
Tudi pri tej definiciji si pomagajmo s sliko. Sedaj opazujmo funkcijske vrednosti, ko se približujemo 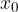z desne. Opazimo, da se funkcijske vrednosti približujejo 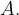Zato je sedaj desna limita v točki 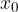enaka
Desna limita: proti x se bližamo z desne strani
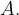
Naj bo 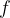definirana v okolici točke . 
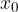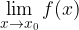obstaja natanko tedaj, ko obstajata leva in desna limita in sta enaki:
Zvezna funkcija
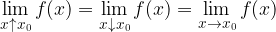
Na zgornji sliki vidimo, da je funkcija zvezna, saj je za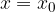 
funkcija definirana. Če se približujemo k 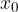z desne ali leve opazimo, da se funkcijske vrednosti približujejo isti vrednosti (leva in desna limita sta enaki).
Do nezveznosti lahko pride pri prehodu iz ene funkcije v drugo.
Za primer nezveznosti si poglejmo funkcijo signum (funkcijo predznaka), ki je definirana kot:
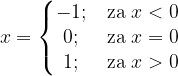
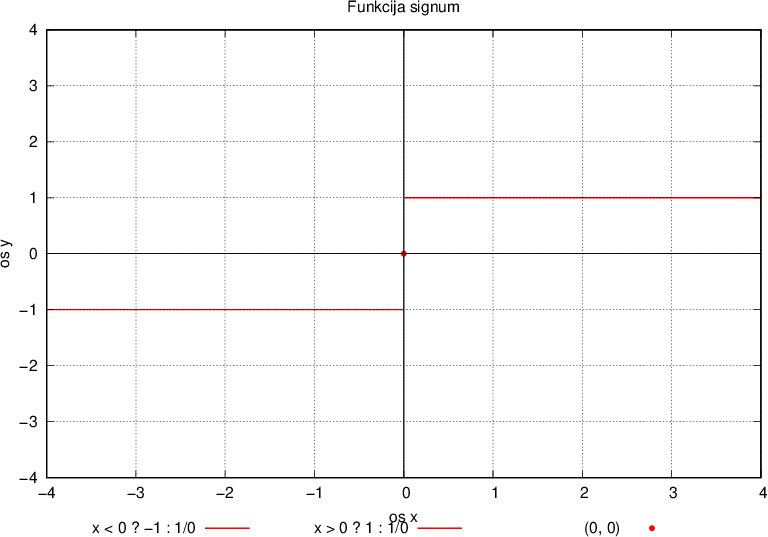
Ta funkcija je sicer povsod definirana, vendar pa v točki 0 ni zvezna - graf se tam pretrga.
Nekatere zvezne funkcije, ki so zvezne na vsem definicijskem območju so:
Kostantna funkcija: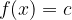 
Linearna funkcija: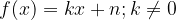 
Kvadratna funkcija: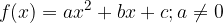 
Potenčna funkcija z naravnim eksponentom: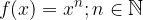 
Polinomi: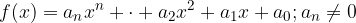 
Eksponentna funkcija: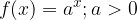 
Logaritemska funkcija: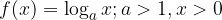
Sinusna funkcija: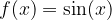 
Kosinusna funkcija: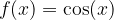 
Če sta funkciji 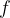in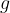 
zvezni funkciji v točki 
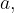so njuna vsota (razlika) 
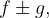produkt 
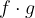in kvocient 
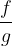(če je 
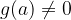) tudi zvezne funkcije v točki 
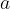in velja:
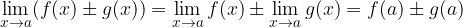
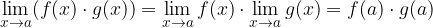
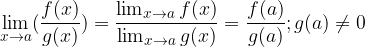
- Zvezna funkcija, ki ni nikjer na zaprtem intervalu enaka 0, ima na vsem intervalu stalen predznak (je povsod pozitivna ali povsod negativna).
- Če je na krajiščih zaprtega intervala 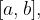na katerem je zvezna, različno predznačena, ima na tem intervalu vsaj eno ničlo.
- Funkcija, ki je zvezna na zaprtem intervalu, je na njem omejena in zavzame svojo natančno zgornjo mejo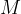 
in spodnjo mejo 
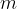in vse vrednosti med njima.
- Če je funkcija 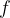naraščajoča in zvezna, je njena inverzna funkcija 
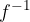tudi zvezna in naraščajoča funkcija.
