Osebne zbirke
Prijava z e-naslovom
Prijava brez gesla
Adicijski izreki nam povejo, kako lahko preoblikujemo:
kotno funkcijo nekega ne-osnovnega kota
v izraz s kotnimi funkcijami osnovnih kotov.
S pojmom osnovni koti imamo v mislih kote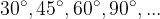 
.
Vrednost izraza znamo nato izračunati s pomočjo tabele vrednosti sinusov in kosinusov.
Osnovne adicijske izreke lahko uporabimo, ko znamo kot v argumentu kotne funkcije zapisati kot vsoto ali razliko osnovnih kotov.
Sinus vsote / razlike kotov
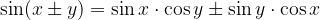
Kosinus vsote / razlike kotov
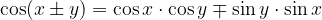
Tangens vsote / razlike kotov
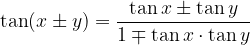
Pogosto so močno orodje pri poenostavljanju trigonometričnih izrazov, reševanju enačb, pri računanju natančnih vrednosti nekaterih kotov, izpeljevanju formul in podobno.
Naj navedemo formule za preoblikovanje kotne funkcije dvojnih kotov. Vse spodnje formule lahko izpeljemo iz gornjih adicijskih izrekov.
Sinus dvojnega kota
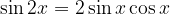
Kosinus dvojnega kota
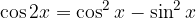
Tangens dvojnega kota
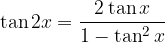
Sinus polovičnega kota:
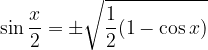
Kosinus polovičnega kota:
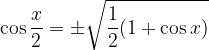
Tangens polovičnega kota:
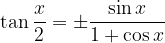
S pomočjo adicijskih izrekov izpeljimo formuli za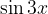 
in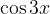 
.
Preoblikujmo:
Preoblikujmo:
Lahko zapišemo:
Sinus trojnega kota je enak:
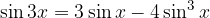
Kosinus trojnega kota je enak:
