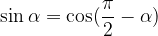Osebne zbirke


Trigonometrija je veja matematike, ki se ukvarja s kotnimi funkcijami. Kotne ali trigonometrične funkcije, so matematične funkcije, katerih vrednosti funkcije odvisne od kota.
Trigonometrija se je razvila iz proučevanja trikotnikov (pravokotnih), odnosov med stranicami in koti v pravokotnem trikotniku in s proučevanjem podobnih trikotnikov.
Osnovne in najpogosteje uporabljane trigonometrične funkcije so:
Kote lahko merimo z dvema različnima merama:
stopinjah:
celoten krožni lok šteje 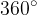 , oziroma, ena stopinja šteje
, oziroma, ena stopinja šteje 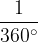 celotnega krožnega loka;
celotnega krožnega loka;
radianih:
celoten krožni lok šteje 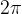 , oziroma, ena stopinja šteje
, oziroma, ena stopinja šteje 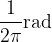 celotnega krožnega loka.
celotnega krožnega loka.
Ker z različnimi merami opisujemo isti pojem, sta meri med seboj povezani:
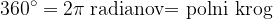
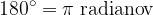
Pri računanju uporabljamo približek 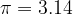 .
.
Formula za pretvarjanje kotov iz radianov v stopinje:
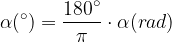
Formula za pretvarjanje stopinj v radiane:
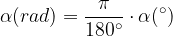
Enotska krožnica je množica točk, ki so za 1 enoto oddaljene od koordinatnega izhodišča. Uporabljamo jo za prikaz vrednosti kotnih funkcij.
Ne glede na to, katero točko na enotski krožnici (z izhodiščem v središču) gledamo, vsaka ima koordinati, ki ju zapišemo kot:
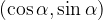
Narišimo si poljuben kot, v našem primeru 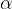 , in v presečišču kota in enotske krožnice si označimo točko, v našem primeru C. Za vsako točko na enotski krožnici vemo, da:
, in v presečišču kota in enotske krožnice si označimo točko, v našem primeru C. Za vsako točko na enotski krožnici vemo, da:
x = koordinata, ki predstavlja vrednost kosinusa kota
y = koordinata, ki predstavlja vrednost sinusa kota
Kote, ki so večji od 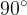 in manjši od
in manjši od 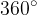 , najlažje prevedemo v ostre kote po obrazcih:
, najlažje prevedemo v ostre kote po obrazcih:
''Lepi'' koti so:
večkratniki kota 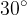
večkratniki kota 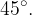
Vrednosti 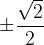 se pojavita izključno pri simetralah kvadrantov (to so koti
se pojavita izključno pri simetralah kvadrantov (to so koti 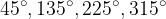 ).
).
Vrednosti ''lepih'' kotov lahko preberemo v enotski krožnici:
Vrednosti, ki si jih moramo zapomniti, so naštete v naslednji tabeli:
Ko pogledamo tabelo, ugotovimo, da se od 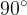 naprej vrednosti sinusa in kosinusa ponavljajo:
naprej vrednosti sinusa in kosinusa ponavljajo:
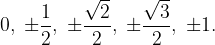
Vrednosti preostalih kotov, ki jih lahko izpeljemo s pomočjo predhodne tabele:
Tudi ko pogledamo skico v poglavju Prehod na ostre kote, ugotovimo, da imata kota 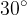 in
in 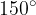 res enako vrednost.
res enako vrednost.
Na osnovi tabele lahko določimo tudi predznake sinusa in kosinusa v kvadrantih (ker sta sinus in kosinus zamaknjena za 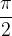 , lahko enako zamaknjenost opazimo tudi v predznačenosti):
, lahko enako zamaknjenost opazimo tudi v predznačenosti):
Tabela vrednosti kotnih funkcij tangens (tan x) in kotangens (cot x) se da najlažje izpeljati s formulami:
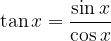
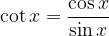
Ko tabelo pogledamo, ugotovimo, da se vrednosti tangensa in kotangensa od  naprej ponavljajo:
naprej ponavljajo:
Ko upoštevamo še zvezi 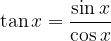 in
in 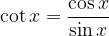 ter predznake sinusov in kosinusov, zlahka napišemo še tabelo predznakov za tangens in kotangens.
ter predznake sinusov in kosinusov, zlahka napišemo še tabelo predznakov za tangens in kotangens.
Vse vrednosti kotnih funkcij ostalih ''nelepih'' kotov računamo s kalkulatorjem. Na enotski krožnici jih lahko določimo samo zelo približno.
Spodnje zveze se uporabljajo pri poenostavljanju izrazov in za reševanje trigonometričnih enačb:
Tangens in kotangens
Iz gradiva Funkciji tangens in kotangens že poznamo zvezi:
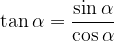
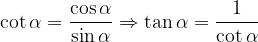
Pitagorov izrek
Prav tako nam je iz gradiva Funkciji sinus in kosinus znan Pitagorov izrek:
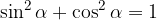
Zveza med kosinusom in tangensom
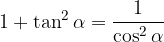
Zvezo lahko z nekaj premetavanja hitro izpeljemo:
Zveza med sinusom in kotangensom
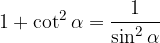
Zvezo lahko hitro izpeljemo:
Komplementarna kota sta kota, za katera velja: 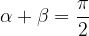 .
.
Spreminjanje kosinusa v sinus:
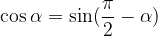
Spreminjanje sinusa v kosinus: