Osebne zbirke


Za uvod si zastavimo vprašanje: ali je zračni tlak kaj odvisen od hitrosti gibanja zraka - vetra? Odgovor je pritrdilen. Ko veter zapiha v ožine npr. med stolpnice mesta, se mu hitrost poveča, tlak pa zmanjša. To je nekoliko presenetljivo, saj je v nasprotju z našimi izkušnjami: čim večja je gneča v ožini, bolj se ljudje prerivajo, večji je tlak med njimi.
Omenjeno zakonitost opisuje Bernoullijeva enačba. V tem gradivu jo bomo izpeljali s pomočjo energijske enačbe:
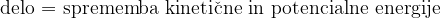
Zavedamo se, da velja zgornja enačba le za togo telo (telo, ki se pod vplivom sile ne deformira). To ne velja za tekočine, zato pričakujemo, da bo izpeljana enačba v realnosti precej nenatančna. Da bi enačba veljala vsaj približno, moramo zagotoviti nekatere pogoje.
Bernoullijeva enačba je zato izpeljana ob naslednjih predpostavkah (nezani pojmi so razloženi v nadaljevanju):
tok tekočine (kapljevine ali plina) je laminaren;
zanemarimo stisljivosti tekočine (plina);
tekočina se med gibanjem ne segreva zaradi zunanjega vira toplote;
trenje med molekulami tekočine (viskoznost) in med cevjo in tekočino je zanemarljivo
Molekule tekočin se gibljejo po tirih, ki se imenujejo tokovnice. Tokovnice omejuje tokovna cev. To so mejne tokovnice, znotraj katerih opazujemo tok. Primer tokovnic, z označeno tokovno cevjo, je na sliki 2:
Gostejše tokovnice pomenijo pomenijo hitrejši tok. Tok je hitrejši, ko je manjši presek cevi.
Predno pa zapišemo Bernoullijevo enačbo, najprej spoznajmo naslednje pojme:
laminarni in turbulentni tok,
stacionarni tok,
viskoznost tekočin.
Glede na tire gibanja ločimo laminarni in turbulentni tok - slika 3.
Pri laminarnem toku tečejo tokovnice druga ob drugi; se ne vrtinčijo, molekule med seboj ne trkajo in se ne ovirajo pri gibanju - slika 3 levo.
Če ima cev povsod enak presek (kot na sliki 3), je tudi hitrost molekul na vsaki tokovnici enaka. Lahko pa se spreminja hitrost med tokovnicami. Ob robu cevi je manjša kot na sredi. Vzrok je viskoznost - trenje med cevjo in tekočino ter med molekulami tekočine. Pri izpeljavi Bernoullijeve enačbe bomo to razliko zanemarili.
Pri vrtinčnem ali turbulentnem toku (slika 3 - desno) so tokovnice nepravilnih oblik in se časovno neprestano spreminjajo. Tokovnica kaže smer delcev tekočine v izbranem trenutku. Že naslednji trenutek se tokovnica spremeni in s tem se menja tudi smer gibanja delcev.
Stacionarni tok je tok, v katerem se hitrosti delcev (v poljubni opazovani točki) vzdolž toka s časom ne spreminjajo.
Da bo tok stacionaren, morata biti izpolnjena dva pogoja:
volumenski tok mora biti konstanten;
tok ne sme biti turbulenten.
Pri stacionarnem toku se vektor hitrosti delcev tekočine s časom ne spreminja. Pogoj za to je, da je volumenski tok konstanten in da se tekočina ne vrtinči.
Poglejmo si natančneje oba pogoja:
Volumenski tok je konstanten
Spomnimo se: volumenski tok nam pove, kolikšen volumen tekočine preteče skozi izbran presek cevi v določenem času. Zapišimo to:
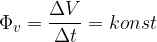
Enačbo za konstantni volumenski tok volumenski tok lahko zapišemo še v obliki:
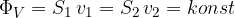
kjer je S presek skozi tok in v hitrost tekočine skozi ta presek.
Konstantnost pretoka ni odvisna od laminarnosti ali turbulentnosti samega toka ali pa viskoznosti tekočine. Zgornja enačba velja v vseh teh primerih, le da moramo upoštevati povprečne hitrosti delcev skozi izbran presek:
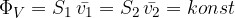
Tok ni turbulenten
Ta pogoj velja čisto po definiciji: v stacionarnem toku se hitrosti delcev ne spreminjajo, kar pa ni res za turbuletni tok.
Vzrok za viskoznost je notranje trenje med molekulami tekočine. Vzemimo primer gibajoče tekočine v cevi - slika 3 levo. Njena največja hitrost je na sredini cevi. Preko notranjega trenja v tekočini se hitrost prenača iz hitrejše plasti na počasnejšo. Plasti tekočine vzdolž celotnega preseka potujejo z različnimi hitrostmi. Plast tekočine, ki se nahaja tik ob cevi, se prilepi na cev, njena hitrost je nič.
Trenje med delci tekočin opravlja negativno delo in manjša kinetično energijo gibajoče se tekočine.
Viskoznost je podrobneje opisana v gradivu Viskoznost.
Viskoznost opisuje notranje trenje med delci gibajoče tekočine. Zaradi vpliva viskoznosti je tok najhitrejši na sredini cevi, tik ob cevi pa pade na nič.
Bernoullijeva enačba povezuje tlak in hitrost delcev tekočine v cevi, kjer se pretaka idealna tekočina. Idealna tekočina je:
nestisljiva in
ima viskoznost nič.
Ker ni notranjega trenja med delci tekočine (viskoznost je enaka nič), se tekočina tudi ne bo segrevala. Predpostavimo, da tudi ni zunanjega vira toplote oziroma da je cev v toplotno izolirani posodi. Tok naj bo laminaren.
Idealna tekočina je nestisljiva tekočina z viskoznostjo nič.
Izpeljimo Bernoullijevo enačbo. Pri tem si pomagamo s skico z nagnjeno cevjo kot kaže slika 6:
Na levi strani bata, s silo F, delujemo na ploskev s ploščino 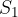 . S tem ustvarjamo tlak:
. S tem ustvarjamo tlak:
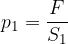
Zaradi delovanja sile se bat in tekočina pod batom premakneta s hitrostjo 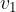 za
za 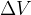 . Pri tem naj bo težišče tega dela tekočine na višini
. Pri tem naj bo težišče tega dela tekočine na višini 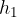 .
.
Za enak volumen se premakne tudi tekočina v spodnjem, ožjem delu cevi, saj je tekočina nestisljiva. Opazovani odsek je na višini 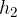 . Hitrost
. Hitrost 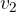 je večja od
je večja od 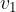 , saj velja enačba za kostantnost volumenskega toka:
, saj velja enačba za kostantnost volumenskega toka:
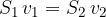
Kolikšen je tlak 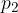 ?
?
Izhajamo iz energijske enačbe: delo tlaka je enako spremembi kinetične in potencialne energije:
Dobili smo Bernoullijevo enačbo. Členi v enačbi so:
p je statični tlak;
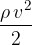 je dinamični tlak ali gostota kinetične energije;
je dinamični tlak ali gostota kinetične energije;
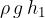 je gostota potencialne energije.
je gostota potencialne energije.
Bernoullijeva enačba pravi: v idealni tekočini je vsota statičnega tlaka, dinamičnega tlaka in gostote potencialne energije znotraj tokovne cevi in vzdolž tokovnice konstantna. Če te količine opazujemo na dveh mestih, velja:

Čim večja je kinetična energija (hitrost) in (ali) potencialna energija (višina), tem manjši je tlak.
V strugi reke je pravokotni kvader, npr. nosilec mostu (slika 8). Nosilec predstavlja oviro na poti vode. Ploščina, ki jo nastavlja toku je S. Daleč pred oviro je hitrost reke 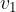 in tlak gibajoče vode
in tlak gibajoče vode 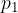 . Hidrostatični tlak zanemarimo. Ko tok vode zadane ob oviro, se ob njej ustavi. Hitrost vode pravokotno na oviro odnosno gostota kinetične energije je tu nič, tlak pa
. Hidrostatični tlak zanemarimo. Ko tok vode zadane ob oviro, se ob njej ustavi. Hitrost vode pravokotno na oviro odnosno gostota kinetične energije je tu nič, tlak pa 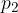 . Razliko obeh tlakov
. Razliko obeh tlakov 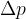 imenujemo zastojno tlak. Silo, s katero nosilec ovira tok pa opisuje kvadratni zakon upora.
imenujemo zastojno tlak. Silo, s katero nosilec ovira tok pa opisuje kvadratni zakon upora.
Na drugi strani ovire se voda vrtinči in odteka naprej.
Zapišimo Bernoullijevo enačbo:
Silo, s katero deluje tok na nosilec, izračunamo iz zastojnega tlaka.
Enaka sila, le nasprotno predznačena, je sila, s katero steber ovira tok. Imenujemo jo sila upora:
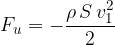
Zapisana enačba ni natančna. V našem primeru smo vzeli za oviro kvader s pravokotnim presekom. Kolikšna je dejansko sila upora, je odvisno od oblike ovire. Zaobjamemo jo v faktorju c, ki predstavlja koeficient upora:
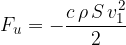
Enačba se imenuje kvadratni zakon upora. V enačbi je S presek ovire, ki ga nastavlja toku, c pa koeficient upora.
Spodnja tabela podaja koeficient upora c za nekatere oblike teles.
Zastojni tlak je nadtlak, ki nastane ob oviri, ob katero zadene tok in zato tam pade hitrost toka na nič. Zastojni tlak izračunamo z enačbo:
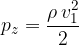
Kvadratni zakon upora opišemo z enačbo:
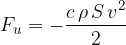
kjer je:
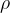 gostota pretakajoče tekočine,
gostota pretakajoče tekočine,
S presek ovire, pravokotne na smer toka,
v hitrosti toka daleč od ovire,
c koeficient upora, ki je odvisen od oblike telesa (ovire).