Prijava z e-naslovom
Prijava brez gesla
Z binomskim izrekom se srečamo že v osnovni šoli, ko spoznamo, da je:
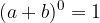
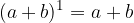
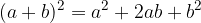
Slednje imenujemo kvadrat dvočlenika. V 1. letniku srednje šole nato spoznamo še kub dvočlenika:
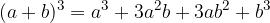
Naša želja je, da bi spoznali, kako na enostaven način izračunati dvočlenik na višjo potenco, torej splošno:
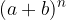
To naredimo z binomskim izrekom.
Poglejmo, kako bi koeficiente, ki nastopajo pri razvoju potence dvočlenika, kar se da hitro izračunali.
Izpolnimo spodnjo tabelo za določene vrednosti eksponenta:
Ko smo tabelo izpolnili, smo dobili v tretjem stolpcu števila zapisana v obliki trikotnika. Tak trikotnik imenujemo Pascalov trikotnik.
Opazimo, da je seštevek dveh sosednjih členov vedno enak členu, ki se nahaja med členoma v naslednji vrstici.
Pri kombinacijah smo se že srečali z binomskim simbolom, kar nam bo zagotovo v pomoč pri binomskem izreku.
Ponovimo, binomski simbol:
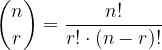
kjer je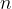 
število vseh elementov med katerimi izbiramo, 
pa število elementov s katerimi ustvarjamo različne kombinacije.
Z n označimo množico vseh elementov, ki so nam na razpolago, r pa nam pove število elementov, s katerimi sestavljamo različne kombinacije.
Binomski simbol zapišemo:
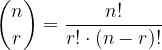
Pri binomskem izreku bomo uporabljali zapise binomskega simbola, zato bomo posebej pogledali nekatere lastnosti binomskega zapisa.
Spomnimo se:
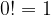
Vemo, da je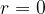 
in 
:
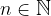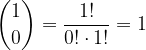
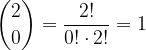
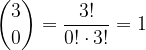
Vrednost binomskega izreka, ko je :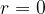
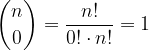
Vemo, da je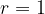 
in :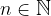
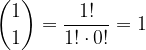
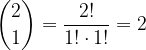
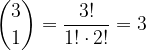
Vrednost binomskega izreka, ko je :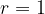
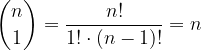
Vemo, da je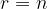 
:
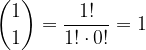
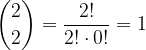
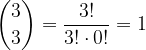
Vrednost binomskega izreka, ko je :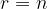
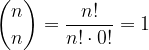
Binomska simbola sta enaka, če je vsota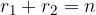 
, torej:
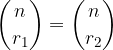
Dokaz:
Ker pri množenju velja zakon o zamenjavi, lahko vidimo, da sta leva in desna stran zapisa enaka. Pri pogoju 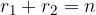torej velja:
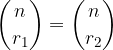
Binomska simbola
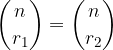
sta enaka, kadar je vsota .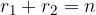
To lahko zapišemo tudi na naslednji način:
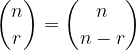
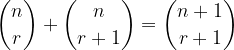
Dokaz:
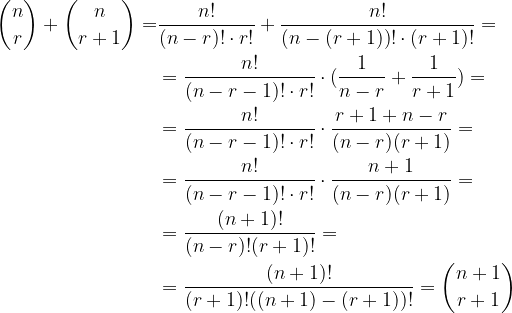
Poglejmo Pascalov trikotnik s koeficienti in z binomskimi simboli:
Če si sedaj ogledamo to preglednico, vidimo, da 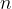predstavlja določen eksponent, pa poteka od 
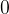do 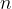. Tako lahko zapišemo splošni binomski izrek za poljubno potenco:
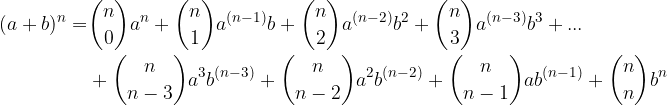
Želimo izračunati:
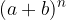
in pri tem si bomo pomagali z binomskim izrekom, ki se glasi:
