Osebne zbirke


Povedano najenostavneje so cela števila samo razširjena naravna števila in sicer k množici naravnih števil, dodamo še 0 in negativna naravna števila. Množico celih števil označujemo z:
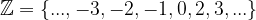
ali
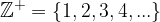 , kar je ravno
, kar je ravno 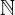
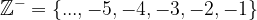
in vidimo, da je 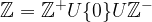 in pravimo, da je množica naravnih števil sestavljena iz množice pozitivnih celih števil (kar je enako množici naravnih števil), množice negativnih celih števil in števila nič.
in pravimo, da je množica naravnih števil sestavljena iz množice pozitivnih celih števil (kar je enako množici naravnih števil), množice negativnih celih števil in števila nič.
Ker so cela števila samo razširjena naravna števila jih lahko upodobimo kar na isti številski premici. Razširimo jo tako, da vsa naravna števila prezrcalimo preko izhodišča - enoto nanašamo še levo od izhodišča.
Premico z naravnimi števili podaljšamo v levo:
eno enoto v levo dobimo število 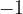
eno enoto v levo od števila 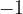 dobimo število
dobimo število 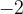
postopek ponavljamo, tako da enakomerno nanašamo enoto v levo in tako dobimo še ostala števila
Število 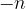 imenujemo nasprotna vrednost števila
imenujemo nasprotna vrednost števila 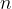 . Naravnim številom rečemo pozitivna cela števila, prezrcaljenim naravnim številom pa negativna cela števila.
. Naravnim številom rečemo pozitivna cela števila, prezrcaljenim naravnim številom pa negativna cela števila.
Seštevanje in množenje celih števil definiramo podobno kot seštevanje in množenje naravnih števil. Zraven teh dveh osnovnih računskih operacij, pa v množici celih števil definiramo tudi odštevanje.
Odštevanje definiramo kot prištevanje nasprotne vrednosti: 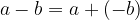 , pri čemer ševilo
, pri čemer ševilo 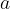 imenujemo zmanjševanec, število
imenujemo zmanjševanec, število 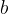 odštevanec in število
odštevanec in število 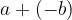 razlika.
razlika.
Za cela števila zraven lastnosti računskih operacij naravnih števil, velja še nekaj zakonitosti.
Pri prištevanju števila 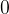 se rezultat ne spremeni.
se rezultat ne spremeni.
Nevtralni element za seštevanje:
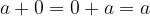
za vsak 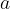 iz
iz 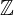
Vsota poljubnega celega števila in njemu nasprotnega števila je enaka 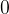 .
.
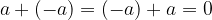
Nasprotna vrednost števila 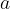 je število
je število 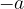 .
.
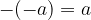
Nasprotna vrednost vsote je enaka vsoti nasprotnih vrednosti.
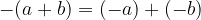
Število 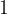 je nevtralni element za množenje.
je nevtralni element za množenje.
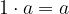
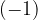
Pri množenju števila 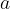 s številom
s številom 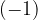 dobimo nasprotno vrednost števila
dobimo nasprotno vrednost števila 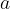 .
.
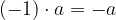
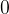
Pri množenju poljubnega števila s številom 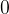 je rezultat vedno enak
je rezultat vedno enak 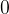 .
.
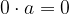
Produkt sodo mnogo negativnih faktorjev je pozitiven.
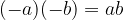
Produkt liho mnogo negativnih faktorjev je negativen.
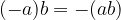
Pri računanju upoštevamo vrstni red računskih operacij (množenje ima prednost pred seštevanjem in odštevanjem), v primeru oklepajev pa vedno najprej odpravimo le te. Pri tem moramo biti pozorni na predznake:
Če je pred oklepajem znak plus (+) in oklepaj izpustimo, števila v oklepaju ohranijo svoj predznak:
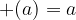
in
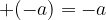
Če je pred oklepajem znak minus (-) in oklepaj izpustimo, števila v oklepaju spremenijo svoj predznak:
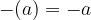
in
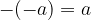
V množici celih števil lahko poljubni dve števili primerjamo med seboj in ugotovimo ali sta enaki (=) oziroma katero od njiju je večje (>) oziroma manjše (<). V množici naravnih in celih števil pa je definirana še relacija manjše ali enako (<=) oz. večje ali enako (>=).
Za poljubni celi števili 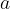 in
in 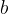 velja, da je
velja, da je 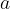 večje od
večje od 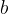 , kar s simboli zapišemo:
, kar s simboli zapišemo:
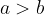
če in samo če je
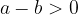
oziroma, če število 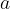 leži na desni strani števila
leži na desni strani števila 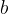 .
.
Za poljubni celi števili 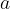 in
in 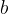 velja, da je
velja, da je 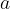 manjše od
manjše od 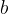 , kar s simboli zapišemo:
, kar s simboli zapišemo:
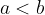
če in samo če je
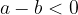
oziroma, če število 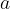 leži na levi strani števila
leži na levi strani števila 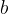 .
.
Za poljubni celi števili 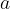 in
in 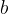 velja, da je
velja, da je 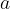 enako
enako 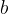 , kar s simboli zapišemo:
, kar s simboli zapišemo:
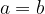
če in samo če je
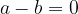
oziroma, če število 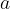 sovpada s številom
sovpada s številom 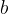 .
.
Za poljubni celi števili 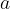 in
in 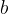 velja, da je
velja, da je 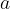 manjše ali enako
manjše ali enako 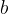 , kar s simboli zapišemo:
, kar s simboli zapišemo:
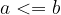
če in samo če je
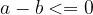
oziroma, če število 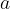 leži na levi strani števila
leži na levi strani števila 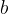 ali z njim sovpada.
ali z njim sovpada.
Za poljubni celi števili 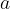 in
in 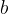 velja, da je
velja, da je 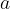 večje ali enako
večje ali enako 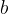 , kar s simboli zapišemo:
, kar s simboli zapišemo:
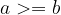
če in samo če je
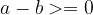
oziroma, če število 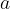 leži na desni strani števila
leži na desni strani števila 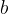 ali z njim sovpada.
ali z njim sovpada.
Če na obeh straneh neenakosti prištejemo isto število se neenakost ohrani:
če je
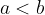
potem je tudi
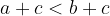
Relacija "manjše" je tranzitivna:
če 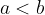 in
in 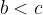 potem je tudi
potem je tudi 
Pri množenju neenakosti s pozitivnim številom, se znak neenakosti ohrani:
če je 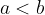 in
in 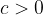 potem je
potem je 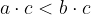
Pri množenju neenakosti z negativnim številom, pa se znak neenakosti obrne:
če je 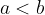 in
in 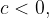 potem je
potem je 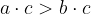
Relacija "manjše ali enako" je refleksivna:
če je 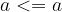
Relacija "manjše ali enako" je antisimetrična:
če je 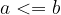 in
in 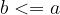 , potem je
, potem je 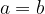
Relacija "manjše ali enako" je tranzitivna:
če je 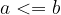 in
in 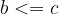 , potem je
, potem je 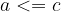
Relacija "večje ali enako" je refleksivna:
če je 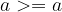
Relacija "večjee ali enako" je antisimetrična:
če je 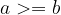 in
in 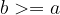 , potem je
, potem je 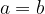
Relacija "večje ali enako" je tranzitivna:
če je 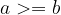 in
in 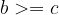 , potem je
, potem je