Prijava z e-naslovom
Prijava brez gesla
O deliteljih govorimo, če lahko eno število delimo z drugim številom. V tem primeru pri deljenju ni ostanka.
Če račun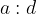 
nima ostanka, potem je število 
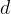delitelj števila 
.
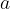Število ima lahko več deliteljev:
Delitelj števila 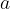je vsako število 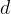, pri čemer velja, da je količnik 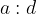naravno število, ostanek pa je enak 0.
Delitelje števila 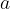zapišemo kot množico, ki jo označimo z 
.
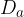Pri iskanju deliteljev določenega števila nam ni potrebno deliti z vsemi naravnimi števili od 1 do tega števila, ampak si lahko pomagamo na način, opisan v naslednjem primeru:
Vsako število ima končno število deliteljev, posebej pa omenimo dva izmed njih:
najmanjši delitelj je število 1, saj 1 deli vsa naravna števila.
največji delitelj pa je število samo.
Števila, ki imajo natanko ta dva delitelja, imenujemo praštevila. Števila s tremi ali več delitelji pa so sestavljena števila.
Število 1 ima le enega delitelja, ki je hkrati njegov najmanjši in največji delitelj, zato število 1 ni ne praštevilo, ne sestavljeno število.
Števila, ki delijo več različnih števil, imenujemo skupni delitelji teh števil.
Skupni delitelji števil 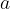in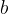 
so vsa tista števila, s katerimi sta hkrati deljiva 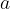in .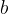
Vsako število ima končno število deliteljev, zato lahko množici nekih števil določimo tako najmanjši kot največji skupni delitelj.
Najmanjši delitelj vsakega števila je 1, zato je 1 tudi najmanjši skupni delitelj več števil.
Najmanjši skupni delitelj dveh ali več števil je število 1.
Najmanjši skupni delitelj dveh ali več števil je vedno število 1, zato to za nas ni zanimivo. Zanimiv pa je največji skupni delitelj. Največji skupni delitelj množice števil je največje število, ki hkrati deli vsa izmed števil v tej množici.
Največji skupni delitelj števil označimo z veliko tiskano črko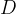 
, ki ji sledi oklepaj, v katerega navedemo ta števila.
Največji skupni delitelj števil 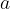in 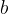zapišemo kot 
.
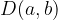Če iščemo največji skupni delitelj večjih števil, bi iskanje vseh deliteljev postalo zamudno. Zato si pomagamo z razcepom števil na prafaktorje.
Največji skupni delitelj množice števil je torej število, sestavljeno iz prafaktorjev, ki so hkrati vsebovani v vsakem številu te množice.
Največji skupni delitelj množice števil je število, sestavljeno iz vseh skupnih prafaktorjev števil v množici.
Če se isti prafaktor ponovi večkrat, ga tudi v izračunu upoštevamo večkrat. Pri zapisu s potenco to pomeni, da vzamemo najnižjo potenco posameznega prafaktorja, ki se ponovi v vseh podanih številih.
Če množica števil nima nobenega večjega skupnega delitelja od 1, števila v tej množici imenujemo tuja si števila.
Števila, katerih skupni delitelj je zgolj število 1, imenujemo tuja si števila.
