Osebne zbirke


Določeni integral se uporablja za izračun ploščine krivočrtnega lika, ki ga na izbranem intervalu omejujeta nenegativna zvezna funkcija in abscisna os.
Označimo ga kot:
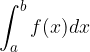
kjer je 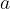 spodnja meja in
spodnja meja in 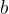 zgornja meja določenega integrala.
zgornja meja določenega integrala.
To poglavje je namenjeno učencem, ki jih zanima teoretično ozadje. Učenci, ki se želijo naučiti praktične uporabe določenega integrala, lahko to poglavje izpustijo.
V koordinatnem sistemu vzemimo lik, ki je omejen z abscisno osjo, grafom zvezne funkcije 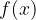 in premicama
in premicama 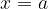 in
in 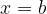 .
.
Razdelimo interval 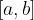 na n podintervalov:
na n podintervalov:
Širine podintervalov so:
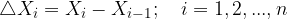
V vsakem podintervalu izberemo točko z absciso 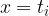 tako, da velja:
tako, da velja:
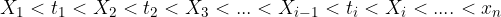
Narišemo pravokotnike z višino 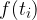 .
.
Produkt 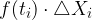 je ploščina pravokotnika označenega na zgornji sliki
je ploščina pravokotnika označenega na zgornji sliki
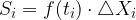
Če seštejemo ploščine vseh pravokotnikov, dobimo približek za ploščino lika, ki ga omejuje funkcija 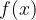 ter premici
ter premici 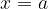 in
in 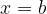 :
:
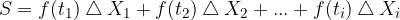
Tem ožji so pasovi, torej čim manjše so ploščine pravokotnikov, tem bolj se vsota ploščin približa ploščini krivočrtnega lika na intervalu 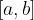 . Natančna ploščina lika je vrednost limite:
. Natančna ploščina lika je vrednost limite:
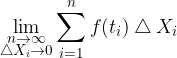
Limito imenujemo določeni integral.
Določeni integral funkcije 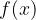 na intervalu
na intervalu 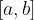 je limita vsote
je limita vsote
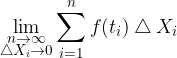
ko gredo širine vseh delnih intervalov 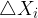 proti
proti 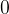 , (pri enakomerni delitvi intervala velja
, (pri enakomerni delitvi intervala velja 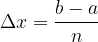 , ki pri limitiranju teži proti 0), število delilnih točk n pa proti neskončnosti:
, ki pri limitiranju teži proti 0), število delilnih točk n pa proti neskončnosti:
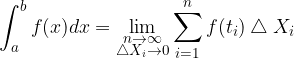
Število 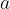 je spodnja meja, število
je spodnja meja, število 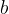 pa zgornja meja določenega integrala.
pa zgornja meja določenega integrala.
V tem poglavju je nakazan geometrijski pomen nedoločenega integrala. Različni primeri računanja likov so obravnavani nekoliko kasneje.
Določeni integral zvezne funkcije 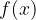 na intervalu
na intervalu 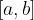 je enak ploščini lika, omejenega s krivuljo
je enak ploščini lika, omejenega s krivuljo 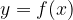 in abscisno osjo na intervalu
in abscisno osjo na intervalu 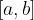 :
:
Določeni integral, oziroma ploščino označenega lika, označimo z:
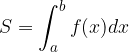
Med nedoločenim in določenim integralom velja zveza, ki jo imenujemo Newton-Leibnizova formula ali osnovni izrek integralskega računa:
Če je funkcija 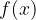 zvezna na intervalu
zvezna na intervalu 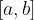 in je
in je 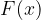 poljuben nedoločeni integral funkcije
poljuben nedoločeni integral funkcije 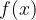 :
:
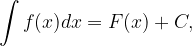
potem velja:
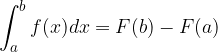
kar zapišemo tudi:
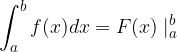
Določeni integral je razlika nedoločenih integralov na zgornji in spodnji meji.
V praksi to pomeni, da določeni integral funkcije 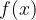 na intervalu
na intervalu 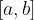 lahko torej izračunamo tako, da najprej integriramo
lahko torej izračunamo tako, da najprej integriramo 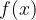 . Dobimo funkcijo
. Dobimo funkcijo 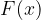 , ki je nedoločeni integral funkcije
, ki je nedoločeni integral funkcije 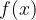 . Od vrednosti funkcije
. Od vrednosti funkcije 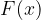 na zgornji meji
na zgornji meji 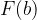 odštejemo vrednost na spodnji meji
odštejemo vrednost na spodnji meji  .
.
Določeni integral vsote dveh funkcij je enak vsoti določenih integralov posameznih funkcij.
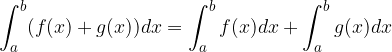
Če je 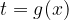 odvedljiva funkcija na intervalu
odvedljiva funkcija na intervalu 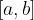 potem velja:
potem velja:
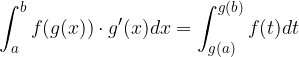
Naj bo 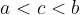 . Tedaj velja:
. Tedaj velja:
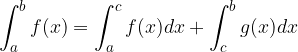
Naj bo 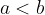 . Če določenemu integralu zamenjamo meji med seboj, integral spremeni predznak.
. Če določenemu integralu zamenjamo meji med seboj, integral spremeni predznak.
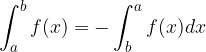
Če sta meji enaki, ima nedoločeni integral vrednost 0.
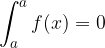
Konstantni faktor, s katerim je pomnožena funkcija pod integralskim znakom, lahko pišemo pred integralski znak:
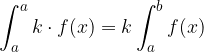
Če je funkcija 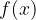 na intervalu
na intervalu 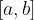 zvezna, obstaja na tem intervalu vsaj ena točka
zvezna, obstaja na tem intervalu vsaj ena točka  , tako da je
, tako da je
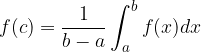
Število 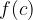 imenujemo povprečna vrednost funkcije na izbranem intervalu.
imenujemo povprečna vrednost funkcije na izbranem intervalu.
Povprečna vrednost funkcije 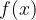 na intervalu
na intervalu 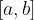 je:
je:
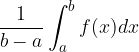
Določeni integral zvezne funkcije 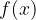 na intervalu
na intervalu 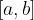 je enak ploščini lika, omejenega s krivuljo
je enak ploščini lika, omejenega s krivuljo 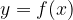 in abscisno osjo na intervalu
in abscisno osjo na intervalu 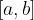 :
:
Določeni integral označimo z:
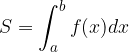
Imejmo primer, ko je funkcija 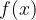 na intervalu
na intervalu 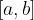 zvezna in povsod negativna
zvezna in povsod negativna 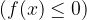 :
:
Določeni integral
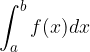
je zato tudi negativen in enak nasprotni vrednosti ploščine lika, omejenega z grafom funkcije 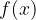 ter premicama
ter premicama 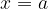 in
in 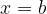 :
:
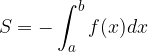
Da bo izračunan določeni integral enak ploščini lika, funkcijo zapišemo z absolutno vrednostjo:
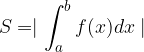
Imejmo primer, ko je funkcija 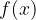 na intervalu
na intervalu 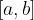 zvezna ter pozitivna in negativna:
zvezna ter pozitivna in negativna:
Določeni integral
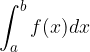
je enak razliki med ploščinami likov, ki ležijo nad abscisno osjo in ploščinami likov, ki ležijo pod abscisno osjo (liki so omejeni z grafom funkcije in abscisno osjo). Da bo izračunani določeni integral enak ploščini označenega lika, funkcijo zapišemo s pomočjo podintervalov:
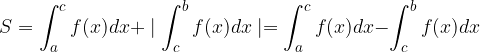
Prav tako kot računanje ploščin likov, ki jih grafi oklepajo z osjo x, lahko računamo tudi ploščine likov, ki ležijo med dvema grafoma.
Naj bosta dani funkciji 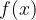 in
in 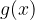 :
:
Ploščino lika, ki ga določata grafa zveznih funkcij 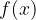 in
in 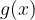 na intervalu
na intervalu 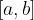 , kjer za vsak
, kjer za vsak 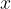 iz tega intervala velja
iz tega intervala velja 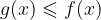 , izračunamo kot:
, izračunamo kot:
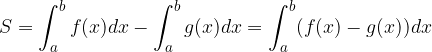
Poglejmo si primer podrobneje.
Naj bosta funkciji 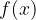 in
in 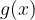 zvezni na intervalu
zvezni na intervalu 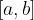 . Graf funkcije
. Graf funkcije 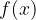 naj leži nad grafom funkcije
naj leži nad grafom funkcije 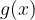 za vsak
za vsak 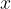 iz tega intervala:
iz tega intervala:
Izračunati želimo ploščino lika, ki ga omejujeta grafa funkcij 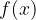 in
in 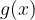 na intervalu
na intervalu 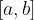 :
:
Poglejmo najprej ploščino lika, ki ga omejujeta krivulja 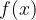 in abscisna os.
in abscisna os.
Na intervalu 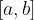 je ploščina lika med grafom funkcije
je ploščina lika med grafom funkcije 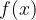 in abscisno osjo, glede na geometrijski pomen določenega integrala enaka:
in abscisno osjo, glede na geometrijski pomen določenega integrala enaka:
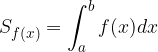
Podobno določimo ploščino lika med grafom funkcije 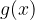 in abscisno osjo.
in abscisno osjo.
Ploščina tega lika je tako:
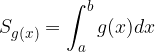
Iščemo ploščino lika, ki se nahaja med obema krivuljama.
Iz slike je razvidno, da je ploščina lika med obema grafoma enaka:
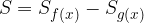
Kar lahko zapišemo tudi drugače:
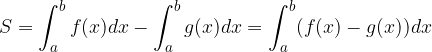
Naj bosta dani funkciji 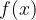 in
in 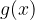 :
:
Če leži kateri od grafov funkcij 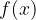 in
in 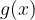 na integracijskem intervalu
na integracijskem intervalu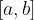 pod abscisno osjo, prištejemo obema funkcijama isto, dovolj veliko pozitivno konstanto
pod abscisno osjo, prištejemo obema funkcijama isto, dovolj veliko pozitivno konstanto 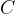 , da oba grafa premaknemo nad abscisno os.
, da oba grafa premaknemo nad abscisno os.
Tako dobimo funkciji 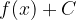 in
in 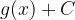 , pri tem pa se lik, katerega ploščino bi radi izračunali, ne spremeni (ostane skladen s prvotnim). Ploščino osenčenega lika tako lahko izračunamo:
, pri tem pa se lik, katerega ploščino bi radi izračunali, ne spremeni (ostane skladen s prvotnim). Ploščino osenčenega lika tako lahko izračunamo:
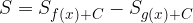
Ploščina med grafom funkcije 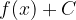 in abscisno osjo je:
in abscisno osjo je:
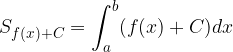
Ploščina med grafom funkcije 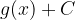 in abscisno osjo pa je:
in abscisno osjo pa je:
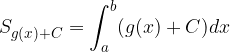
Ploščino lika med obema grafoma lahko sedaj zapišemo:
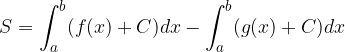
Ob upoštevanju, da je integral vsote funkcij enak vsoti integralov funkcij, vidimo, da se v računu konstanta 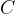 izniči in je ploščina osenčenega lika enaka:
izniči in je ploščina osenčenega lika enaka:
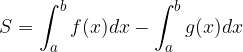
Če območje, ki ga omejujeta graf funkcije 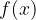 in os
in os 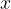 na intervalu
na intervalu 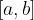 zavrtimo za
zavrtimo za 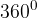 okoli abscisne osi, dobimo rotacijsko telo.
okoli abscisne osi, dobimo rotacijsko telo.
Prostornino vrtenine, kjer funkcijo 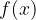 zavrtimo za
zavrtimo za 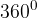 okoli abscisne osi, izračunamo s pomočjo določenega integrala:
okoli abscisne osi, izračunamo s pomočjo določenega integrala: