Prijava z e-naslovom
Prijava brez gesla
Da bomo lažje razumeli, kaj je električna potencialna energija, se spomnimo najprej na mehansko potencialno energijo. Mehansko potencialno energijo (slika 1 levo), dobi:
telo z maso m,
ko ga dvignemo na višino h,
v težnem ali gravitacijskem polju z gravitacijskim pospeškom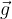 
.
Mehanska potencialna energija je enaka delu, ki smo ga opravili, da smo dvignili telo na to višino:
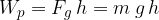
Pri tem:
predstavlja prvi faktor maso m (torej lastnost samega telesa),
produkt gh pa nam pove, pri kolikšnem gravitacijskem pospešku in na kakšno višino smo prestavili telo.
Analogno dobimo električno potencialno energijo (slika 1 desno), ko:
naboj e,
prestavimo iz točke, kjer je električna potencialna energija nič, v končno točko (opravimo pot s),
Ker moramo pri tem premagati električno silo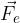 
, na poti s opravimo delo, ki je enako prejeti električni potencialni energiji. Če nato naboj spustimo, na njega deluje samo električna sila. Naboj se zato giblje v smeri sile vzdolž silnic, električna potencialna energija pa se mu manjša.
Slika 1: mehanska (levo) in električna (desno) potencialna energija.
Električna potencialna energija je torej odvisna od dela, ki ga opravimo (ali pa ga opravi električno polje), ko premaknemo naboj iz ene točke v drugo. Delo je odvisno od:
velikosti naboja e,
poti s, ki smo jo opravili vzdolž silnic in
Delo je enako električni potencialni energiji, ki jo prejme naboj.
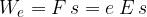
Pri tem:
predstavlja prvi faktor naboj e (torej lastnost samega telesa),
produkt Es pa imenujemo električni potencial (analogno bi lahko poimenovali produkt gh mehanski potencial) in ga označimo z V:
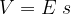
Razliko dveh potencialov imenujemo napetost in jo označimo z U. Več o tem pa v nadaljevanju.
Podobno kot pri mehanski potencialni energiji lahko tudi tukaj poljubno izberemo ploskev s potencialno energijo nič. Kakšna je smiselna izbira se bomo naučili v nadaljevanju.
Naj bo pozitivni naboj e v točki A, v homogenem električnem polju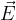 
. Na naboj deluje električna sila 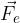, usmerjena vzdolž silnic električnega polja. Naboj premaknemo proti smeri silnic v točko B in C. Pri tem moramo delovati s silo F, ki je nasprotna električni sili, s katero deluje električno polje na naboj. Premik naredimo po treh različnih poteh, kot kaže slika 2.
Slika 2: med dvema ekvipotencialnima ploskvama je delo sile neodvisno od poti.
Delo, ki smo ga opravili, ni odvisno od dolžine poti. Če potujemo iz točke A v točko B po najkrajši možni poti s v nasprotni smeri silnic, premagujemo največjo možno silo:
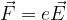
in opravimo delo:
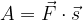
Delo je vedno enako skalarnemu produktu vektorja sile in poti. Če premaknemo naboj po daljši pot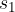i 
ali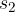 
, je komponenta sile, ki jo moramo premagati, manjša. V vsaki točki gibanja moramo upoštevati le tisto komponento sile, ki je v smeri poti. Skupno delo pa je v vseh primerih enako (glej sliko 2).
Z delom smo nabitemu telesu povečali energijo, ki ji pravimo električna potencialna energija. Oznaka za električno potencialno energijo je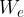 
. Pri tem je Delo:
pozitivno, če premaknemo pozitivni naboj proti polju ali negativni naboj v smeri polja;
negativno, če električno polje premakne pozitivni naboj v smeri silnic ali negativni naboj proti silnicam električnega polja.
V vsakem primeru pa je delo enako spremembi električne potencialne energije:
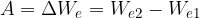
Pomudimo se še pri sliki 2. Opazimo dve črtkani črti (rjave barve), pravokotni na silnice električnega polja:
prva gre skozi točko A,
druga pa skozi točki B in C.
Ti črti predstavljata ploskvi (če si črtkani črti predstavljamo kot ploskvi, ki se širita v in ven iz zaslona) in jima pravimo ekvipotencialni ploskvi.
Lastnost ekvipotencialne ploskve je, da:
imajo vse točke na določeni ekvipotencialni ploskvi enak potencial (kaj je potencial se bomo naučili nekoliko nižje);
je vedno pravokotna na silnice električnega polja.
Iz obeh lastnosti sledi, da če naboj premaknemo:
iz poljubne točke prve ekvipotencialne ploskve na poljubno točko, ki leži na drugi ekvipotencialni ploskvi, opravimo vedno enako delo.
po isti ekvipotencialni ploskvi, ne opravljamo nobenega dela, saj sta v tem primeru sila in pot med seboj pravokotni pravokotni (skalarni produkt pravokotnih vektorjev je vedno nič).
Delo je enako spremembi električne potencialne energije:
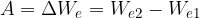
Električna potencialna energija naboja se poveča, če opravimo pozitivno delo (delo je pozitivno, če smo ga opravili mi) in pa zmanjša če opravimo negativno delo.
Podobno kot pri mehanski potencialni energiji lahko tudi zdaj izberemo poljubno ekvipotencialno ploskev, na kateri naj bo električna potencialna energija naboja nič. Praktično to naredimo tako, da npr. na izbrano ploskev položimo kovinsko ploščo in jo ozemljimo (glej sliko 4). Ozemljitev pomeni, da jo povežemo na vodnik, ki ima na drugi strani npr. kovinsko ploščo, zakopano v zemlji.
Slika 4: ozemljena ekvipatencialna ploskev.
V tem primeru lahko izračunamo električno potencialno energijo, ki jo ima naboj po naslednjem postopku:
Pozitivni električni naboj postavimo na ozemljeno ekvipotencialno ploskev.
Premaknemo ga vzdolž silnic v točko, kjer želimo izračunati električno potencialno energijo.
Če smo naboj premaknili:
v nasprotno smer električnega polja (slika 4, levo), smo pri premiku opravili delo in je energija naboja pozitivna.
v smeri električnega polja (slika 4, desno), smo delo prejeli in je energija naboja negativna.
Električno potencialno energijo izračunamo po enačbi:
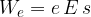
kjer je s najkrajša razdalja med izbrano točko in ekvipotencialno ploskvijo z izbrano ničelno energijo.
Če je naboj negativen, je razmišljanje podobno. Upoštevati moramo le, da je smer električne sile nasprotna smeri električnega polja.
Ekvipotencialna ploskev je ploskev, ki je pravokotna na silnice električnega polja. Če premaknemo naboj iz poljubne točke prve ekvipotencialne ploskve na poljubno točko neke druge ekvipotencialne ploskve opravimo vedno enako delo. Če premikamo naboj po sami ekvipotenvialni ploskvi, ne opravimo nobenega dela.
Delo sile, ki premakne naboj iz ene ekvipotencialne ploskve na drugo, je neodvisno od poti, pač pa samo od razdalje med ekvipotencialnima ploskvama. Z delom spreminjamo električno potencialna energijo. Izračunamo ga kot:
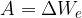
V homogenem električnem polju lahko izberemo poljubno ekvipotencialno ploskev in ji pripišemo nični potencial. V tem primeru je električna potencialna energija naboja, ki se nahaja na razdalji s:
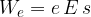
Električna potencialna energija je lahko pozitivna ali negativna. Če mi opravimo delo, ko premaknemo naboj vzdolž silnic v električnem polju, je pozitivna, če opravi delo električno polje, pa negativna.
Pravokotno na silnice električnega polja postavimo kovinsko ploskev in jo ozemljimo. Naboj, ki se bi nahajal na njej, bi imel električno potencialno energijo nič.
Zapišimo zdaj električni potencial za naboj, ki se nahaja na razdalji s od ozemljene plošče. Pri tem vemo, da:
ima naboj električno potencialno energijo, ki je sorazmerna velikosti naboja, pa tudi produktu Es;
produkt Es označimo z V.
Začnimo z enačbo, da je delo enako spremembi električne potencialne energije:
Enota za potencial je volt [V]:
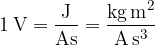
Točka v polju E ima potencial 1V, če opravimo delo 1J, ko premaknemo naboj 1As iz ravnine s potencialom 0 do izbrane točke.
V homogenem električnem polju računamo električni potencial točke po enačbi:
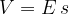
Pri tem je s najkrajša razdalja med točko in ploskvijo s potencialom nič. Enota za električni potencial je volt [V]:
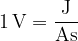
Električni potencial ima isti preznak kot električna potencialna energija pozitivnega naboja v izbrani točki.
Električno potencialno energijo in električni potencial v okolici točkastega naboja e dobimo, če izračunamo delo, ki ga moramo opraviti, da premaknemo naboj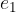 
:
od točke (ploskve), kjer je električna potencialna energija nič,
do izbrane točke v električnem polju (glej sliko 6).
Slika 6: električna potencialna energija v okolici točkastega naboja.
V primeru točkastega naboja je smiselno izbrati za izhodiščno ravnino, kjer je električna potencialna energija nič, kroglo z radijem neskončno. Pri tej razdalji je tudi električna poljska jakost nič, saj pada s kvadratom razdalje od naboja (glej teorijo Električna poljska jakost).
Kogar zanima, je izpeljava enačb v naslednjem podpoglavju. Tu samo povzamemo rezultat:
Potencialna energija naboja 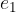, ki se nahaja na razdalji r okoli točkastega naboja, je:
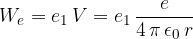
Potencial na razdalji r pa je:
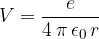
Električna poljska jakost E v okolici točkastega naboja e ni konstantna. Pada s kvadratom razdalje r od naboja e, ki jo povzroča. Zato moramo pri izračunu dela razdeliti pot na majhne odseke, znotraj katerih smatramo, da je E konstantna (glej sliko 7) in izračunati prispevek dela za vsak odsek:
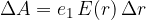
Pri tem upoštevamo, da je električna polska jakost okoli točkastega naboja sorazmerna naboju e, ki jo povzroča in obratno sorazmerna kvadratu razdalje:
Slika 7: izračun električne potencialne energije v okolici točkastega naboja.
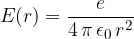
Odseke seštejemo od radija, kjer je električna potencialna energija enaka nič, pa do izbrane točke.
Izberemo si lahko poljubno ekvipotencialno ploskev, na kateri bi imel naboj e potencialno energijo nič. Ta ploskev bi lahko bila tudi površina zelo velike kovinske in ozemljene krogle, ki obkroža naboj. A če si predstavljamo osamljen naboj, brez preprek, njegovo električno polje pade na nič šele v neskončnosti. To praktično pomeni, da moramo seštevati majhne odseke (modre pravokotničke s slike 7) do neskončnosti.
Seštevanje odsekov izvedemo z določenim integralom. Ne da bi integral računali (za napredne učence je to narejeno v naslednjem podpoglavju), zapišimo rezultat:
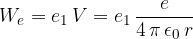
Pri tem je električni potencial točke na razdalji r od naboja e:
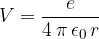
To poglavje je namenjeno učencem, ki so že osvojili integrale. Učenci, ki ne poznajo integralov lahko to poglavje brez škode preskočijo.
Računanja ploščine pod grafom funkcije, kot je nakazano na sliki 4, se lotimo z integralom. Pri tem znak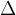 
, ki je simbol za "veliko razliko" (natančneje: ne-infinitezimalno razliko) zamenjamo z neskončno majhno razliko, ki jo označimo z d (diferencial).
Uporabimo enačbo:
Delo je enako električni potencialni energiji:
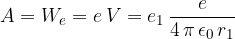
Pri tem je električni potencial na razdalji r od naboja e enak:
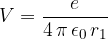
Električna napetost je razlika dveh potencialov. Spomnimo se: potencial računamo ali merimo med izbrano točko in zemljo. Če imamo več točk z različnimi potenciali, je med njimi napetost (glej sliko 5).
Oznaka za napetost je U, enota pa enaka kot za potencial: volt [V].
Ker nam je iz vsakdanjega življenja bolj domača beseda napetost, lahko tudi rečemo: potencial je napetost proti zemlji in napetost je razlika potencialov.
Primerjavo med električno potencialno energijo, potencialom in napetostjo prikazuje slika 5. Črtkane vodoravne črte na sliki prestavljajo ekvipotencialne ploskve:
Slika 5: električna potencialna energija, potencial in napetost
Delo sile pri prestavljanju naboja e iz prve ekvipotencialne ploskve na drugo je (glej sliko 5):
Zgornjo enačbo lahko zapišemo tudi v obliki:
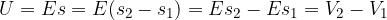
Pri tem sta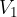 
in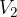 
potenciala obeh ravnin.
Napetost je razlika potencialov med dvema točkama ali ekvipotencialnima ploskvama:
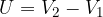
Napetost izračunamo tudi iz zveze:
