Prijava z e-naslovom
Prijava brez gesla
Tako kot poznamo v matematiki množenje med števili, poznamo tudi množenje med vektorji. Množenje dveh vektorjev poimenujemo skalarni produkt.
Da je definicija množenja med vektorji, kot jo bomo zapisali, pravilna, se izkaže po tem, da se dobesedno zlije z ostalimi spoznanji v matematiki - npr. Pitagorovim izrekom. Pitagorov izrek je posledica množenja dveh, med seboj pravokotnih, vektorjev.
Naj bosta dana vektorja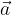 
in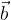 
, ki imata skupno začetno točko in oklepata kot 
.
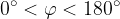Skalarni produkt dveh vektorjev je enak produktu velikosti prvega in drugega vektorja ter kosinusa vmesnega kota:
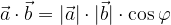
Rezultat skalarnega množenja je realno število oziroma skalar.
Iz obrazca za skalarni produkt:
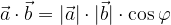
lahko hitro razberemo kdaj je skalarni produkt enak 0. To bo takrat, ko bo vsaj eden od vektorjev in ničelni vektor ali ko je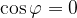 
. To pa je takrat, ko sta vektorja pravokotna (
).
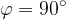Če vektor 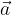skalarno pomnožimo s samim seboj, je kot 
:
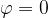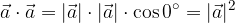
Dolžino vektorja 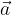je zato enaka:
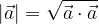
Izračun dolžine vektorja, ki je podan s komponentami, je podan v gradivu Skalarni produkt v pravokotnem koordinatnem sistemu. Tukaj pa si poglejmo preprost primer.
Pravokotna projekcija vektorja 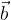na vektor (
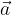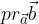) je daljica, ki jo dobimo, če začetno in končno točko vektorja 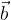pravokotno projiciramo na vektor .
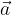Ko vektor 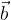pravokotno projiciramo na vektor 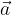, dobimo pravokotni trikotnik s hipotenuzo 
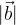in kateto .
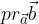V pravokotnem trikotniku uporabimo kotno funkcijo kosinus:
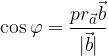
iz dobljene zveze izrazimo:
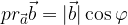
Dobljeno zvezo vstavimo v formulo za skalarni produkt:
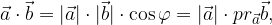
kar lahko zapišemo kot:
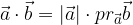
Skalarni produkt dveh vektorjev je enak produktu dolžine prvega vektorja in pravokotne projekcije drugega vektorja na prvi vektor.
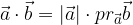
Za skalarno množenje velja zakon o zamenjavi ali komutativnost:
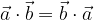
Za skalarno množenje velja zakon o razčlenjevanju ali distributivnost:
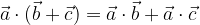
Skalarni produkt je homogen:
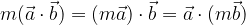
Kosinusni izrek pogosto uporabljamo pri razreševanju poljubnega trikotnika. Tukaj si bomo pogledali izpeljavo kosinusnega izreka z vektorji.
V poljubnem trikotniku označimo stranice z vektorji 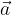, 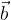in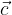 
, ter kot 
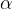(glej sliko).
Vektor 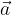izrazimo z vektorjema 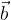in :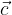
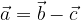
Preoblikujmo zapisano enačbo:
Dobili smo kosinusni izrek. Ekvivalentno lahko izpeljemo kosinusni izrek za vse tri stranice trikotnika.
Kosinusni izreki za vse tri stranice v poljubnem trikotniku so:
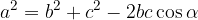
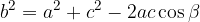
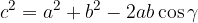
Pitagorov izrek je samo posebna oblika kosinusnega izreka. Oglejmo si, kaj se zgodi s kosinusnim izrekom, če obravnavamo pravokotni trikotnik, kjer je c hipotenuza, a in b pa sta kateti:
Izpeljimo Pitagorov izrek iz kosinusnega izreka:
Izpeljava Pitagorovega izreka s pomočjo skalarnega produkta (skalarni produkt smo uporabili pri izpeljavi kosinusnega izreka) je dodaten dokaz, da je definicija skalarnega produkta, kot smo jo navedli, pravi način, kako množimo vektorje med seboj.
