Osebne zbirke


Gibanje je spreminjanje lege telesa v času. Telo se lahko giblje po
premici (1 dimenzionalni prostor);
ravnini (2 dimenzionalni prostor);
prostoru (3 dimenzionalni prostor).
Glede na hitrost delimo gibanje na:
enakomerno gibanje (hitrost je stalna - konstantna);
neenakomerno gibanje (hitrost ni stalna, temveč se s časom spreminja).
Glede na tir gibanja delimo gibanje na:
premo gibanje;
krivo gibanje.
Telo, ki se giblje, opravi pot. Razlikovati moramo med pojmom poti (označimo jo npr. z s) in lege telesa (označimo jo lahko npr. z x). Med gibanjem se pot, ki jo opravimo, s časom vedno veča. To pa ne velja za našo lego. Lego običajno določamo kot razdaljo do točke, kjer je bilo izhodišče naše poti.
Za enakomerno gibanje velja, da je pot, ki jo opravi telo enaka produktu hitrosti in časa:

V enačbi (1), ko smo zapisali s, smo zares imeli v mislih opravljeno pot, kar pomeni, da nas zanima razlika med končno in začetno točko na tiru gibanja:
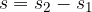
kjer je 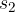 točka, kjer pot nehamo meriti in
točka, kjer pot nehamo meriti in 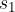 točka, kjer pot začnemo meriti (glej sliko 3). Da bi poudarili, da gre za razliko med končno in začetno točko, v enačbi (1) namesto s pišemo
točka, kjer pot začnemo meriti (glej sliko 3). Da bi poudarili, da gre za razliko med končno in začetno točko, v enačbi (1) namesto s pišemo 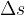 , oziroma:
, oziroma:
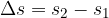
Enako velja za čas:
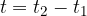
kjer je  točka, kjer čas nehamo meriti in
točka, kjer čas nehamo meriti in  točka, kjer čas začnemo meriti (glej sliko 3). Zato v enačbi (1) tudi čas t nadomestimo z
točka, kjer čas začnemo meriti (glej sliko 3). Zato v enačbi (1) tudi čas t nadomestimo z 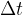 :
:
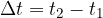
Enačbo (1) v splošni obliki zapišemo kot razliko poti 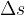 v opazovanem času
v opazovanem času 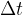 :
:

Izrazimo še hitrost:
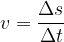
V večini primerov moramo pri nalogah uporabiti osnovne merske enote, torej pot s ima enoto meter m, enota časa je sekunda s in enota za hitrost meter na sekundo m/s. V kolikor so količine v kateri drugi enoti, jih pri reševanju vaj najprej pretvorimo v osnovne enote.
Premo gibanje opazujmo v x, y koordinatnem sistemu. Začetno razdaljo od koordinatnega izhodišča označimo z 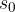 , čas, ko se telo začne gibati pa s
, čas, ko se telo začne gibati pa s 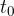 . Opazujmo, kako se s časom t spreminja razdalja s predmeta od koordinatnega izhodišča. Ker je to premo gibanje, se razdalja od izhodišča linearno spreminja s časom.
. Opazujmo, kako se s časom t spreminja razdalja s predmeta od koordinatnega izhodišča. Ker je to premo gibanje, se razdalja od izhodišča linearno spreminja s časom.
Zapišimo še enkrat enačbo 2:
Odvisnost razdalje predmeta od koordinatnega izhodišča in od opazovanega časa zapišemo s splošno enačbo:
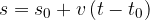
kjer je:
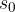 je razdalja predmeta od koordinatnega izhodišča v začetku gibanja.
je razdalja predmeta od koordinatnega izhodišča v začetku gibanja.
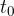 čas, ko se telo začne gibati.
čas, ko se telo začne gibati.
Predmet najprej postavimo v koordinatno izhodišče in poglejmo, kako se mu oddaljenost spreminja s časom. Uporabimo enačbo (2) in upoštevamo, da je začetna oddaljenost 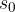 enaka nič in čas, ko se začne predmet gibati
enaka nič in čas, ko se začne predmet gibati 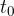 tudi enak nič. Zapišemo enačbo (3):
tudi enak nič. Zapišemo enačbo (3):
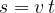
Graf opisanega gibanja je na sliki 4. Hitrost gibanja določa strmino premice. Če bo hitrost večja, bo strmina premice večja kar pomeni, da se bo telo v istem času dlje odmaknilo od izhodišča.
Predmet se nahaja na razdalji 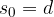 od koordinatnega izhodišča, približevanje predmeta koordinatnemu izhodišču pa začnemo opazovati v času
od koordinatnega izhodišča, približevanje predmeta koordinatnemu izhodišču pa začnemo opazovati v času 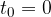 .
.
Enačba (3) se v tem primeru glasi:
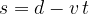
Ker se predmet približuje je predznak hitrosti negativen (in obratno: hitrost je pozitivna, če se predmet oddaljuje), graf s(t) je padajoča funkcija, kot kaže graf na sliki 5.
Kdaj pride predmet v koordinatno izhodišče?
Uporabimo enačbo:
Kaj pa, če se nahaja predmet v izhodišču in se prične gibati v času  ? Enačbo za pot sedaj razdelimo na dva intervala:
? Enačbo za pot sedaj razdelimo na dva intervala:
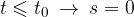
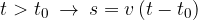
Ali smo drugo enačbo zapisali pravilno? Preverimo:
Če v enačbo vstavimo 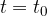 , mora biti razdalja s še vedno nič, saj se je ravno takrat začel predmet premikati:
, mora biti razdalja s še vedno nič, saj se je ravno takrat začel predmet premikati:
Šele, ko je  je
je 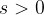 ; telo se prične oddaljevati od izhodišča.
; telo se prične oddaljevati od izhodišča.
Telo se giblje določen čas s hitrostjo 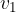 , nato z neko drugo hitrostjo
, nato z neko drugo hitrostjo 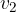 itd. Govorimo o odsekoma enakomernem gibanju. V vsakem odseku se giblje enakomerno, vendar se hitrost gibanja od odseka do odseka menja.
itd. Govorimo o odsekoma enakomernem gibanju. V vsakem odseku se giblje enakomerno, vendar se hitrost gibanja od odseka do odseka menja.
Da si laže predstavljamo tako gibanje, narišemo graf hitrosti v odvisnosti od časa.
Odseke enakomernega gibanje predstavljajo na sliki 9 ravne črte, vzporedne s časovno osjo. V vsakem odseku je hitrost stalna.
Poglejmo prvi odsek na sliki 9. Telo se v času od 0 sekund do 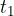 sekund giba s hitrostjo
sekund giba s hitrostjo 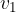 . Pot izračunamo po znani enačbi:
. Pot izračunamo po znani enačbi:
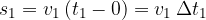
Grafično si predstavljamo pot kot ploščino pravokotnika, na sliki 7 šrafiranega s poševnimi črtami. Podobno bi lahko izračunali pot za vse tri odseke po sliki 9:
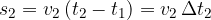
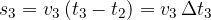
Skupna pot je torej:
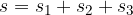
Pot je bila opravljena v času t sekund:
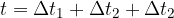
Povprečna hitrost telesa pa je celotna pot deljeno s celotnim časom:
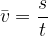
Povprečna hitrost telesa je tista hitrost, ki bi jo moralo imeti telo, če bi se gibalo ves čas enakomerno, da bi opravilo enako pot v enakem času kot pri odsekoma enakomernem gibanju.
Izračunamo jo tako, da seštejemo vse poti in delimo s celotnim časom:
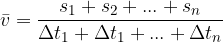
Telo se giblje premo in enakomerno v smeri in s hitrostjo rezultante dveh ali več vektorjev hitrost. Glede na vrsto naloge in našega znanja matematike lahko vektorje seštevamo grafično, geometrično ali s pomočjo kotnih funkcij, Pri naprednem znanju matematike lahko uporabimo tudi vektorski račun (glej Operacije z vektorji).
Kako rešujemo naloge, kjer je hitrost sestavljena iz več komponent, si oglejmo na primeru.