Osebne zbirke


Beseda entropija ima izvor v klasični grščini in pomeni obrat ali spremembo.
Opazujmo spremembe v naravi in vzemimo celotno naravo kot en sam sistem. S pomočjo dela človek spreminja okolje: sezida si hišo, pospravi stanovanje, regulira strugo reke, zgradi tovarno. Zamislimo si, da po končanem delu prepusti rezultat dela naravi. Po dovolj dolgem času bo stanje ponovno enako, kot je bilo pred njegovim posegom. Hiša in tovarna se bosta porušili, reka bo ponovno tekla po strugi, ki si jo bo sama izbrala. Stanje bo na prvi pogled takšno, kot da ni bilo nikakršnega vpliva človeka.
Pa bo stanje res popolnoma enako? Že dejstvo, da je moral za ureditev okolice opraviti delo, za kar je npr. potreboval svojo fizično moč, gradbene stroje itd. nam govori o tem, da stanje ne bo popolnoma enako, kot pred posegom. Če ne drugega, je z delom spremenili notranjo energijo sistema: okolje se je znašlo na višji temperaturi, kot je bilo prej.
V fiziki merjenje takih sprememb označimo s količino, ki ji rečemo entropija; za zgoraj opisani poseg človeka v okolje rečemo, da smo povečali entropijo sistema. Kaj natančno je entropija, bomo spoznali v tem gradivu. Za zdaj je dovolj, če vemo, da je entropija merilo za nakopičene spremembe, ki so se zgodile v sistemu. Oznaka za entropijo je S.
Spontane spremembe v naravi težijo k neurejenosti - k največji možni entropiji. Z vsakim našim posegom v okolico, kjer poskušamo entropijo zmanjšati, povzročimo, da se po spontanih spremembah končna entropija ponovno poveča in to za več, kot nam jo je uspelo zmanjšati. Entropijo kot posledico nakopičenih sprememb nikoli ne moremo zmanjšati, sprememba entropije je večja ali - v idealnem primeru - kvečjemu enaka nič.
Poglejmo še enkrat gornji primer in vzemimo gibanje ene mravlje. Verjetnost, da se bo mravlja znašla spet v isti točki, je precej verjetna. Verjetnost, da pa se bodo vse mravlje istočasno znašle v začetni točki, pa je izredno majhna. A čeprav izredno majhna - je to vseeno situacija, ki je mogoča. Iz povedanega lahko povemo naslednje:
entropija je statistična spremenljivka, v kateri uporabljamo verjetnostni račun;
entropija je lahko kvečjemu 0 (mravlje se spet zberejo v začetnih točkah). Entropija manjša kot 0 v tem primeru niti nima prevelikega smisla, namreč kaj bi pomenilo, da so mravlje "bolj" urejene, kot so bile na začetku?
Če opazujemo spremembe na makroskopskem nivoju, lahko z dokajšnjo gotovostjo zapišemo, da spontane reakcije potekajo samo v eno smer (kot npr. toplotni tok). Spontanim reakcijam, ki potekajo samo v eno smer, pravimo ireverzibilne ali nepovratne spremembe.
Poznamo tudi reverzibilne ali povratne spremembe. Le te so redke, pomembne pa so zato, saj ohranjajo entropijo sistema (v nasprotju z ireverzibilnimi spremembami, ki entropijo sistema večajo).
Spremembe bomo opazovali v sistemu, ki je toplotno izoliran od okolice. S tem bomo dosegli, da opazujemo avtonomen sistem, ki nam da smiselne rezultate. Kaj bi se pa zgodilo, če tega pogoja ne bi postavili? Če opazovani sistem ne bi bil toplotno izoliran od okolice, bi lahko toplota prehajala iz sistema proti okolici. In če bi ta okolica bila npr. na nižji temperaturi, bi se s tem entropija opazovanega sistema zmanjšala. A ta rezultat bi bil posledica dejstva, da v svojih opazovanjih nismo upoštevali okolice. Dobili bi napačen rezultat, ki bi bil posledica nedoslednega opazovanja; namreč, pravi rezultat, v katerem bi opazovali opazovani sistem skupaj z okolico, bi bil povečanje entropije.
Pojem entropije se uporablja v številnih področjih fizike in ostalih področij, kjer imamo opravka z veliko množico dogodkov in kjer velja verjetnostni račun. V tem poglavju se bomo omejili le na področje toplote.
Večina sprememb v naravi je takšnih, da lahko spontano potekajo le v eni smeri. Pravimo jim ireverzibilne spremembe. Le redke spremembe pa potekajo enako v obeh smereh. Pravimo, da so reverzibilne. Pri razumevanju entropije je zelo pomembno, da znamo ločiti reverzibilne spremembe od ireverzibilnih.
Ireverzibilna sprememba je velikokrat posledica trenja med gibanjem telesa.
Mnogo težje kot ireverzibilne je doseči reverzibilne ali povratne spremembe. Vse reverzibilne spremembe se vršijo zelo počasi brez trenja ali upora.
S tem, ko rečemo, da se reverzibilne spremembe dogajajo počasi, to pomeni, da so vsak trenutek vsi deli opazovanega sistema v toplotnem ravnovesju.
Večina sprememb v naravi je ireverzibilnih. Reverzibilne spremembe lahko dosežemo le v redkih primerih in pri skrbnem izvajanju poskusa.
Pogoji za reverzibilno spremembo so:
Spremembo je možno obrniti tako, da je telo na koncu v enakem stanju in isti legi, kot je bil v začetku
Vmesna stanja med prehodi v eno in drugo smer so do potankosti enaka: nasprotno enake hitrosti, enake sile, enake temperature itd. Zdeti se nam mora, kot da smo pri obrnjeni spremembi samo zavrteli film v nasprotno smer.
Med spremembo ni nikakršnega trenja ali upora zraka.
Spremembe potekajo počasi tako, da so med spremembo vsi deli sistema vedno v toplotnem ravnovesju.
Spomnimo se prvega zakona termodinamike. Ta pravi, da je sprememba notranje energije enaka vloženemu delu in dodani toploti:
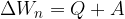
Ta zakon nič ne govori o smeri toplotnega toka. Načelno dopušča tudi možnost, da teče toplota od hladnejšega telesa proti toplejšemu telesu. Hladnejše telo se tako še bolj ohlaja (notranja energija se mu manjša), toplejše telo pa še bolj segreva (notranja energija se mu veča).
Iz izkušenj pa vemo, da sam po sebi takšen tok ni možen, ali pa, da je zelo malo verjeten. Slutimo, da je posredi nov zakon, ki opiše ta pojav. Ta zakon zares obstaja, imenujemo ga pa 2. zakon termodinamike ali entropijski zakon. V najbolj preprosti obliki smo ga spoznali že v uvodu:
Če je telo toplotno izolirano, ga po opravljeni ireverzibilni spremembi ni mogoče več spraviti v prvotno stanje. Pri tem se je telesu povečala entropija.
Kaj pa je entropija in kako jo računamo? Najlaže jo spoznamo s pomočjo plinske enačbe.
Spomnimo se plinske enačbe, ki povezuje tri glavne termodinamične spremenljivke: tlak p, volumen V in temperaturo T:
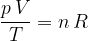
Količnik na levi strani enačbe je za določeno množino plina konstanten. Je enak produktu števila kilomolov n in splošne plinske konstante R.
Do sedaj smo (na idealnem plinu) obravnavali spremembe, kjer je bila ena od spremenljivk konstanta. To so bile:
izotermne spremembe (stalna temperatura),
izobarne spremembe (stalni tlak),
izohorne spremembe (stalni volumen)
Sedaj pa bomo dopustili, da se istočasno spreminjajo tako tlak, volumen kot tudi temperatura.
V isti graf (slika 2) vrišimo:
izotermne spremembe: to so spremembe, ki opisujejo odvisnost tlaka od volumna pri stalni temperaturi (rdeče črte na sliki 2);
adiabatne spremembe: to so spremembe, kjer dopustimo, da se plin med stiskanjem segreva in med razpenjanjem ohlaja (modre črte na sliki 2).
Krivulje, ki označujejo na grafu adiabatne spremembe imenujemo adiabate. Beseda adabata izhaja iz klasične grščine in pomeni neprehoden. Pomeni, da je plin toplotno izoliran, toplota ne more prehajati v okolico.
Na adiabati temperatura raste, če se manjša volumen in veča tlak in obratno: če se veča volumen in manjša tlak temperatura pada.
Pri normalnem zračnem tlaku 1 bar sta točki temperature na izotermi in adiabati identični. Predstavljata (začetno) temperaturo plina, predno ga pričnemo stiskati ali razpenjati. Na adiabatah velja, da se:
med stiskanjem plin segreva. To pomeni dodatno večji tlak, zato je adiabata, za tlake večje od 1 bar, bolj strma od izoterme.
med razpenjanjem plin - pri tlaku pod 1 bar - dodatno ohlaja, zato je lega adiabate tam nižja od izoterme.
Ugotovili smo že (glej primere reverzibilnosti), da so spremembe ob določenih pogojih (počasne spremembe, toplotno izoliran valj z majhno toplotno kapaciteto, ni trenja med batom in valjem) - in jih nakazujejo adiabate - reverzibilne. Pri reverzibilnih spremembah ni spremembe entropije. Adiabate so torej črte, kjer je entropija S konstantna.
Družino krivulj s konstantno temperaturo dobimo tako, da spreminjamo temperaturo plina. Kako pa dobimo družino adiabat?
Ena od možnosti je, da izvedemo ireverzibilno spremembo na plinu in mu s tem povečamo entropijo. A računanje z ireverzibilnimi spremembami je dokaj zapleteno. Zato se problemu izognemo tako, da na določeni temperaturi T plinu dodamo toploto Q (glej sliko 3). S tem plinu spremenimo entropijo za:

Prišli smo do adiabate z nekoliko višjo entropijo. Lahko pa izvršimo spremembo tudi v drugi smeri: plinu odvzamemo toploto in mu s tem zmanjšamo entropijo. Govorimo o reverzibilnih adiabatnih spremembah.
Do enačbe (1) se da priti z matematično izpeljavo ali pa izkustveno. Ugotovili smo, da je količnik 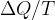 neodvisen od tega, po kateri poti in pri kateri temperaturi prehajamo med adiabatama. Na sliki 3 je tako primer izobarnih (pri stalnem tlaku
neodvisen od tega, po kateri poti in pri kateri temperaturi prehajamo med adiabatama. Na sliki 3 je tako primer izobarnih (pri stalnem tlaku 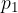 ) in izohornih (pri istem volumnu
) in izohornih (pri istem volumnu 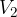 ) prehodov med dvema bližnjima adiabatama.
) prehodov med dvema bližnjima adiabatama.
Pri izobarnih in izohornih prehodih je sprememba entropije enaka, saj pridemo na isto adiabato z višjo entropijo:
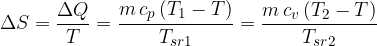
Podobno velja tudi za druge prehode med adiabatoma. Ni važno, po kateri poti in pri kateri temperaturi se vršijo, vedno pridemo na isto adiabato (opomba: več o  in
in  v gradivu Prvi zakon termodinamike).
v gradivu Prvi zakon termodinamike).
Za adiabate velja, da je entropija konstantna.
Vsak ireverzibilni proces povzroči prehod na adiabato z višjo entropijo.
Na adiabato z višjo entropijo lahko pridemo tudi tako, da dopustimo prenos topote Q pri določeni temperaturi T. Med bližnjima adiabatoma, kjer se temperaturi med točkama prehoda le malo razlikujeta, lahko računamo spremembo entropije:
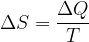
Pri tem ni pomembno, pri kateri temperaturi ali po kateri poti pridemo do bližnje adiabate z višjo entropijo.
Krožna sprememba pomeni, da je naša končna točka potovanja po grafu enaka začetni. Če pri tem potujemo izključno po adiabatah, temu pravimo adiabatna krožna sprememba.
Z dodajanjem in odvzemanjem toplote idealnemu plinu lahko dosežemo reverzibilno adiabatno krožno spremembo. Opazujmo tako krožno spremembo med adiabatami na sliki 4:
Opišimo proces:
Prehod med točko 1 in 2
Iz diabate z nižjo entropijo preidemo na adiabato z nekoliko višjo entropijo tako, da plinu pri določeni temperaturi 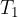 dovedemo toploto
dovedemo toploto 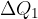 . Pri tem se je tudi temperatura plina nekoliko poveča. Ker je bila dovedena toplota majhna, je bila tudi sprememba temperature majhna, zato lahko računamo z neko srednjo temperaturo ob prehodu
. Pri tem se je tudi temperatura plina nekoliko poveča. Ker je bila dovedena toplota majhna, je bila tudi sprememba temperature majhna, zato lahko računamo z neko srednjo temperaturo ob prehodu 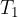 .
.
Prehod med točko 2 in 3
Plin se adiabatno razpenja in opravi delo.
Prehod med točko 3 in 4
Plinu zmanjšamo entropijo tako, da mu pri neki srednji temperaturi 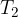 odvzamemo toploto
odvzamemo toploto 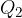 . V trenutku odvzema smo torej začasno prekinili toplotno izolacijo plina, plinu odvzeli toploto in se vrnili na prvotno adiabato.
. V trenutku odvzema smo torej začasno prekinili toplotno izolacijo plina, plinu odvzeli toploto in se vrnili na prvotno adiabato.
Prehod med točko 4 in 1
Plin adiabatno stiskamo. Pri tem opravimo delo, ki je nekoliko manjše od dela pri razpenjanju med točko 2 in 3. Razlika med delom, ki ga odda plin pri prehodu 2 - 3 in delom, ki ga prejme plin pri prehodu 4 - 1 je koristno delo A, ki ga lahko porabimo v primeru toplotnega stroja. Je sorazmerno ploščini zanke na sliki 3.
Še enkrat poudarimo, da je to reverzibilna adiabatna sprememba, kjer se nam po zaključeni poti entropija ohrani. Pri vsaki dodatni ireverzibilnosti se lahko entropija samo poveča:
Carnotova krožna sprememba je krožna sprememba, ki delno potuje po izotermi delno pa po adiabati. Pomembna je zato, ker je Carnotova krožna sprememba osnova za razumevanje toplotnih strojev.
Zamislimo si prehod pri konstantni temperaturi (po izotermi). Če želimo krožne spremembe, potrebujemo dva prehoda:
pri višji temperaturi na adiabato z višjo entropijo
in nazaj pri nižji temperaturi na prvotno adiabato.
Na sliki 5 je prikazana Carnotova krožna sprememba, ki opisuje delovanje toplotnega stroja na osnovi adiabatnih reverzibilnih krožnih sprememb idealnega plina. Kot smo že večkrat omenjali, mora stroj delovati počasi, brez trenja, z majhno toplotno kapaciteto valja in bata in v toplotno izoliranem okolju.
Na sliki 5 so narisane enake izoterme in adiabate, kot so narisane tudi na sliki 2. Opišimo krožno spremembo, kot je naznačena na sliki:
Sprememba 1 - 2
Plin na višji temperaturi 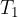 z dodajanjem toplote
z dodajanjem toplote 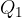 izotermno razpnemo. Poveča se volumen in zniža tlak.
izotermno razpnemo. Poveča se volumen in zniža tlak.
Sprememba 2 - 3
Plin adiabatno razpnemo. V ta namen ga toplotno izoliramo tako, da mu temperatura pade na 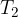 .
.
Sprememba 3 - 4
Plin izotermno stisnemo pri nižji temperaturi 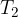 .
.
Sprememba 4 - 1
Plin adiabatno stisnemo tako, da ponovno doseže začetno temperaturo 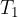 .
.
Zdaj pa to krožno spremembo še matematično opišimo:
Izotermna sprememba 1- 2
Pri izotermni spremembi je dovedena toplota enaka delu, ki ga opravi plin:
Izotermna sprememba 3 - 4
Pri tej spremembi mi opravimo delo in stisnemo plin, zato je predznak negativen. Rezultat je podoben, kot smo ga dobili prej:
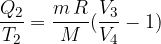
Adiabatna sprememba 2 - 3
Pri adiabatni spremembi je Q konstanten (saj je sistem toplotno izoliran), po prvem zakonu termodinamike je zato sprememba notranje energije enaka delu:
Adiabatna sprememba 4 - 1
Izpeljava je podobna kot za adiabatno spremembo 2 - 3. Dobimo:
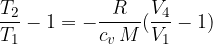
Zapišimo še enkrat enačbo, ki smo jo dobili v adiabatni spremembi 4 - 1:
Sedaj pa zapišimo še enkrat enačbo, ki smo jo dobili pri prehodu 3 - 4:
Dobili smo pomembno zvezo, ki jo bomo s pridom uporabljali pri opazovanju toplotnih strojev. Pri tem še enkrat poudarimo, da morajo biti vse spremembe zelo počasne, tako, da je vsak trenutek plin v toplotnem ravnovesju.
Do iste enačbe pa lahko pridemo tudi tako: na koncu krožne spremembe imajo vse termodinamične spremenljivke enako vrednost. Sprememba entropije je enaka nič:
Za Carnotovo krožno spremembo velja, da je razmerje toplot, ki ju toplotni stroj med krožno spremembo odda ali sprejme enako razmerju temperatur, pri katerih se te spremembe vršijo:
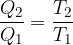
V poglavju Toplotni stroji smo napisali enačbo za izkoristek toplotnega motorja:
Prišli smo do zaključka, da je izkoristek toplotnega motorja, ki deluje po reverzibilnih Carnotovih spremembah enak:
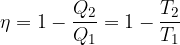
Kaj pa če proces (npr. zaradi trenja bata in valja) ni popolnoma reverzibilen? V tem primeru velja:
Enačbo vstavimo v enačbo za izkoristek toplotnega motorja in dobimo:
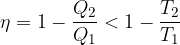
Podobno bi lahko izpeljali tudi za druge toplotne stroje: hladilnik in toplotno črpalko.
Izkoristek toplotnih motorjev je:
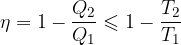
Učinek hladilnih strojev je:
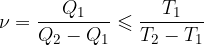
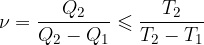
Znak manjši uporabimo, ko so spremembe ireverzibilne.
Zdaj ne bomo več govorili o prehodih med dvema adiabatama, pač pa na splošno med dvema stanjema z različno entropijo. Zapišimo še enkrat enačbo za spremembo entropije; ob tem spomnimo, da enačba ne velja samo za idealni plin, pač pa za poljubno spremembo entropije:
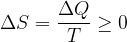
Če je temperaturna razlika med dvema stanjema velika, ne moremo več vzeti srednjo temperaturo prehoda T, kot smo to storili v prejšnjem poglavju. V tem primeru razdelimo prehod na več odsekov s srednjimi temperaturami 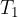 ,
, 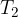 , ...,
, ..., 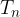 , v vsakem odseku dodamo toploto
, v vsakem odseku dodamo toploto 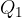 ,
, 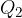 , ...,
, ..., 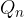 . tem tvorimo količnike, ki predstavljajo majhne deleže entropije in jih seštejemo:
. tem tvorimo količnike, ki predstavljajo majhne deleže entropije in jih seštejemo:
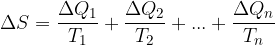
Pri tem smo se intuitivno držali pravila, da se entropije seštevajo.
Ta del je namenjen dijakom, ki so se že naučili osnove integriranja. Vsi ostali ga lahko preskočijo, ne da bi to vplivalo na razumevanje entropije.
Podana je tabela za notranjo energijo 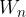 in entropijo S za 1 kg vrele vode in pare pri nasičenem parnem tlaku. Referenčna vrednost notranje energije 0 J in entropije 0 J/K je izbrana pri temperaturi
in entropijo S za 1 kg vrele vode in pare pri nasičenem parnem tlaku. Referenčna vrednost notranje energije 0 J in entropije 0 J/K je izbrana pri temperaturi 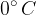 , kjer je nasičen parni tlak 0,0061 bara.
, kjer je nasičen parni tlak 0,0061 bara.