Osebne zbirke
Prijava z e-naslovom
Prijava brez gesla
Funkcijo smo spoznali kot predpis, ki vzame eno število in ga preračuna v drugo število.
Naučili smo se že predstaviti funkcijo z:
enačbo oziroma funkcijskim predpisom,
tabelo,
puščičnim diagramom,
grafom.
Pri tem smo vrednosti spremenljivke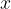 
izbirali zgolj iz množice celih števil. Zanje smo izračunali vrednost funkcije 
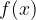in dobili nekaj točk v koordinatnem sistemu.
V praksi pa funkcije pogosto preslikajo vsa realna števila:
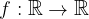
Graf takšne funkcije ni le skupek posameznih točk, temveč sklenjena črta (premica ali krivulja).
Graf funkcije smo obravnavali že v gradivu Funkcija - osnove. Tokrat pa si oglejmo še primer funkcije, ki slika iz realnih števil v realna števila.
Ker taka funkcija določa vrednost za vsa števila, graf ni sestavljen zgolj iz posameznih točk, temveč ima obliko sklenjene črte.
Ko želimo narisati realno funkcijo, bomo za oporne točke naredili tabelo za nekaj števil - običajno vzamemo nekaj celih števil. Funkcija bo preslikala ta cela števila, hkrati pa tudi vsa števila vmes med celimi števili. Za graf torej v koordinatnem sistemu dobimo gosto množico točk v vrsti, drugo ob drugi, kar pa dejansko pomeni črto oziroma krivuljo.
Takšne funkcije, katerih graf je sklenjena črta, pogosto uporabljamo za opisovanje odnosov med količinami.
Pri grafu funkcije sta še posebej pomembni začetna vrednost in ničla funkcije:
začetna vrednost funkcije je vrednost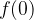 
; na grafu jo prepoznamo kot presečišče z osjo 
,
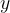ničla funkcije je tista vrednost 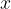, pri kateri velja 
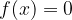; na grafu jo prepoznamo kot presečišče z osjo .
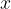Funkcije opisujejo odnose med količinami, ki so medsebojno odvisne. Dva posebna primera takšnih odnosov sta premo sorazmerje in obratno sorazmerje.
Obe vrsti sorazmerja lahko zapišemo kot funkciji, saj vsaki vrednosti neodvisne spremenljivke 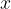pripada točno ena vrednost odvisne spremenljivke .
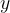Če se pri dvakratnem, trikratnem ... povečanju prve količine druga količina dvakrat, trikrat ... poveča, sta ti dve količini v premem sorazmerju.
Enako velja tudi v obratni smeri. Če se pri dvakratnem, trikratnem ... zmanjšanju prve količine druga količina dvakrat, trikrat ... zmanjša, sta ti dve količini v premem sorazmerju.
Vsako premo sorazmerje lahko zapišemo z enačbo oblike
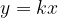
pri čemer:
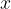predstavlja neodvisno spremenljivko,
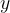je odvisna spremenljivka, ki predstavlja funkcijsko vrednost,
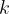pa je koeficient premega sorazmerja
Koeficient premega razmerja je število, ki ga izrazimo kot količnik med funkcijsko vrednostjo 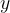in vrednostjo neodvisne spremenljivke :
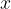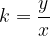
Koeficient premega razmerja je konstanta.
Če vrednost odvisne spremenljivke 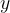zapišemo kot funkcijo neodvisne spremenljivke 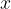, se enačba za premo sorazmerje glasi:
Premo sorazmerje je funkcija, ki jo matematično zapišemo kot:
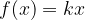
Graf premega sorazmerja je premica, ki poteka skozi izhodišče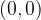 
.
Večji kot je 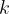, bolj strma je premica.
Če se pri dvakratnem, trikratnem ... povečanju prve količine druga količina dvakrat, trikrat ... zmanjša, sta ti dve količini v obratnem sorazmerju.
Enako velja tudi v obratni smeri. Če se pri dvakratnem, trikratnem ... zmanjšanju prve količine druga količina dvakrat, trikrat ... poveča, sta ti dve količini v obratnem sorazmerju.
Vsako obratno sorazmerje lahko zapišemo z enačbo oblike:
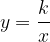
pri čemer:
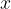predstavlja neodvisno spremenljivko,
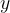je odvisna spremenljivka, ki predstavlja funkcijsko vrednost,
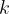pa je koeficient obratnega sorazmerja
Koeficient obratnega razmerja je število, ki ga izrazimo kot produkt funkcijske vrednosti 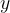in vrednostjo neodvisne spremenljivke :
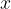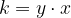
Koeficient obratnega razmerja je konstanta.
Če vrednost odvisne spremenljivke 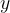zapišemo kot funkcijo neodvisne spremenljivke 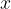, se enačba za obratno sorazmerje glasi:
Obratno sorazmerje je funkcija, ki jo matematično zapišemo kot:
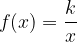
Graf obratnega sorazmerja je krivulja, ki jo imenujemo hiperbola. Hiperbola ima dva kraka, ki sta pri obratnem sorazmerju simetrična glede na koordinatno izhodišče.
