Osebne zbirke
Prijava z e-naslovom
Prijava brez gesla
Naj bo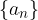 
geometrijsko zaporedje s kvocientom 
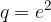in prvim členom 
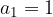. Naj bo dano še zaporedje s splošnim členom 
.
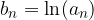Zapišite splošni člen zaporedja 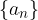in dokažite, da je zaporedje 
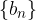aritmetično z diferenco 
.
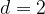Izračunajte vsoto prvih 100 členov zaporedja .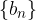
Dokažite, da za poljuben par naravnih števil m, n velja, da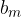 
in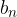 
nista tuji si števili.
Naj bo za vsako naravno število n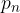 
polinom, definiran s predpisom 
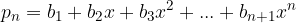. Dokažite, da ima za vsako naravno število n polinom 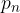na intervalu 
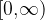natanko eno ničlo.
