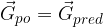Predstavljajmo si nogometaša, ki prestreže žogo in jo preusmeri proti golu (glej sliko 1).
Na žogo je deloval s silo 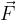 , ki pa je trajala kratek čas
, ki pa je trajala kratek čas 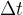 . To je čas, ko je bila žoga v stiku z nogometaševo nogo. Produkt sile in časa imenujemo sunek sile:
. To je čas, ko je bila žoga v stiku z nogometaševo nogo. Produkt sile in časa imenujemo sunek sile:
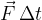
S sunkom sile je torej preusmeril žogo proti golu. Spremenil ji je smer in hitrost gibanja. Pravimo, da ji je spremenil gibalno količino.
Smer in hitrost žoge bi nogometaš težje spremenil, če bi moral brcniti v žogo medicinko. Prav tako je za nogometaša razlika, ali brca v žogo medicinko, ki se premika počasi ali pa hitro. Te izkušnje nam pomagajo razumeti samo gibalno količino: ta je tem večja, čim večja je masa telesa in čim večja je njegova hitrost:
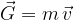
Tudi gibalna količina je vektor. Ima svojo velikost (ki je enaka produktu mase in hitrosti) in tudi smer. Je enako usmerjena kot vektor hitrosti. Zanjo pri seštevanju (ali odštevanju) veljajo enaka pravila računanja z vektorji, kot smo se jih naučili v poglavju Sila kot vektor oziroma v bolj matematičnem gradivo, kjer obravnavamo računske operacije med vektorji.
Sunek sile in sprememba gibalne količine sta tesno povezana in izhajata iz 2. Newtonovega zakona. Poglejmo si to zvezo natančneje.
Na telo z maso m delujemo s silo F. Telo se začne gibati enakomerno pospešeno s pospeškom a:
Tudi prek enačb smo ugotovili to, kar smo slutili že v uvodu: sunek sile (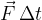 ) je tisti, ki povzroči, da se telesu spremeni gibalna količina (
) je tisti, ki povzroči, da se telesu spremeni gibalna količina (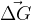 ). Grafično to ponazorimo na sliki 2:
). Grafično to ponazorimo na sliki 2:
Sunek sile je enak spremembi gibalne količine:
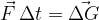
Sprememba gibalne količine je:
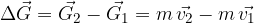
kjer je 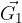 gibalna količina pred delovanjem sunka sile in
gibalna količina pred delovanjem sunka sile in 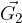 gibalna kopličina po delovanju sunka sile.
gibalna kopličina po delovanju sunka sile.
Izrek o ohranitvi gibalne količine pravi, da se gibalna količina ohrani, če je vsota vseh sunkov sil, ki delujejo na telo, enaka nič. Ohrani se tudi, če telesa med sabo trkajo. A si pogledamo ohranitveni izrek nekoliko podrobneje, spoznajmo:
tipe trkov med delci;
razliko med notranjimi in zunanjimi sunki sil (trki).
Zamislimo si n teles v omejenem prostoru. Vsako telo ima svojo gibalno količino G. Med gibanjem se telesa zadevajo drug ob drugega, pravimo, da trkajo. Trki med telesi so lahko:
prožni
neprožni
delno prožni.
Poglejmo si jih.
Prožni trk (pravimo mu tudi elastični ali idealni trk) je tisti trk, za katerega velja, da se ob trku ohrani celotna kinetična energija.
Neprožni trk je tisti trk, za katerega velja, da se telesi ob trku sprimeta. Kinetična energija teles, ki trčijo, se ne ohrani.
V naravi pa trki niso nikoli popolnoma prožni. Vzemimo žogo in jo spustimo z določene višine. Če bi bila žoga idealno prožna, bi po odboju dosegla enako višino kot je višina, iz katere smo jo spustili (pri tem odmislimo upor zraka). A žoga po vsakem odboju doseže nižjo višino, vse dokler ne obmiruje na tleh. Tak trk je delno prožen, saj se žoga sicer odbije, a se ob vsakem odboju nekaj kinetične energije pretvori v notranjo.
Za primerjavo vzemimo še žogo iz plastelina. Če bi jo spustili na tla, se ta sploh ne bi odbila. Trk žoge iz plastelina s tlemi bi bil neprožen.
Vrnimo se k primeru o biljardu. Da bi lahko določili, kaj je notranja in kaj zunanja sila, moramo najprej določiti kaj je sistem. Izbira sistema je povsem poljubna, navadno sistem izberemo tako, da se nam računi ali pa opazovanje nekega dogajanja najbolj poenostavi.
V primeru biljarda si za sistem izberemo biljardne kroglice. Zdaj, ko smo določili sistem, lahko določimo zunanje in notranje sile:
zunanja sila je vse, kar na izbrani sistem deluje od zunaj. Naštejmo nekaj takih zunanjih sunkov sile:
S palico udarimo eno izmed kroglic: udarec s palico štejemo kot zunanji sunek sile na sistem. Palica ni del našega izbranega sistema in s sunkom kroglicam spremenimo gibalno količino. Če so kroglice pred sunkom npr. mirovale, se zdaj gibljejo.
Kroglica se odbije od roba. Rob ni del našega sistema, zato je delovanje roba na kroglico prav tako zunanji sunek sile na sistem. Namreč tudi v idealnem primeru, ko je trk z robom prožen, se spremeni smer gibalne količine.
Silo trenja med kroglo in podlago tudi štejemo kot zunanjo silo. Podlaga ni del našega sistema, povzroča pa silo trenja, ki manjša skupno gibalno količino.
notranja sila pa je vse, kar se dogaja znotraj sistema. Npr. trk med dvema kroglicama štejemo kot notranji sunek sile, saj sta obe kroglici del našega izbranega sistema.
Poglejmo si natančneje notranji trk. Naj ena krogla trči v drugo:
Ko prva krogla z maso 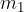 in hitrostjo
in hitrostjo 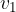 trči ob drugo (glej sliko 5), ki miruje, ji spremeni gibalno količino s sunkom sile:
trči ob drugo (glej sliko 5), ki miruje, ji spremeni gibalno količino s sunkom sile:
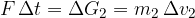
Zaradi vzajemnega delovanja sil, z enakim in nasprotno usmerjenim sunkom sile deluje tudi druga krogla na prvo:
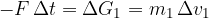
Če seštejemo obe enačbi, dobimo:
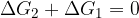
Vidimo, da se je gibalna količina posamezne krogle spremenila, ni pa se spremila skupna gibalna količina.
Zunanji sunki sile spreminjajo celotno gibalno količino teles. V tem jih ločimo od notranjih sunkov sil, ki delujejo med trki. Ti spreminjajo gibalno količino posameznih teles znotraj sistema, vektorska vsota vseh gibalnik količin pa ostaja nespremenjena.
Več gibajočih se teles zaprimo v prostor in pustimo, da med seboj trkajo. Zaradi trkov se spreminjajo smeri in hitrosti gibanja posameznih teles. Ob trkih na posamezna telesa delujejo sunki sile, ki telesom spreminjajo hitrosti in smeri gibanja. A taki sunki sil se zgodijo znotraj zaprtega prostora (znotraj sistema), zato jih imenujemo notranji sunki sil.
Zapišimo izrek o ohranitvi gibalne količine: če od zunaj na telesa ne deluje noben sunek sile, se vsota gibalnih količin vseh teles v sistemu ohrani. Število, velikost in tip notranjih trkov in sil pri tem ni pomembno:
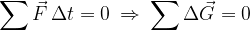
Pokažimo izrek o ohranitvi gibalne količine na primeru neprožnega trka dveh teles. Ker v tem primeru obe telesi predstavljata sistem, je trk med njima notranji in zato na sistem ne deluje nobena zunanja sila. Kolikšni sta gibalni količini pred trkom 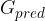 in po trku
in po trku 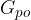 ?
?
Napišimo še enkrat enačbo (1):
Še računsko smo pokazali izrek o ohranitvi gibalne količine.
Če ni zunanje sile, ki bi vplivale na sistem gibajočih teles, se skupna gibalna količina ohranja. Skupna gibalna količina vseh teles po trku je enaka gibalni količini pred trkom: