Osebne zbirke


Osnovni graf sinusa in kosinusa (sinusoida) že znamo narisati.
Pogledali si bomo še transformacije grafov funkcij:
Razteg (skrčitev) vzdolž ordinatne (y) osi
Razteg (skrčitev) vzdolž abscisne (x) osi
Togi premik v smeri ordinatne osi (premik funkcije navzgor ali navzdol po y osi)
Togi premik v smeri abscisne osi (premik funkcije v levo ali desno po x osi)
Vrednost kota α se izraža v radianih. To pomeni, da je vrednost π enaka 3.14159... in ne 180°.
Funkcijo sin x ali cos x pomnožimo z A, kjer 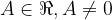 . Dobimo novo funkcijo:
. Dobimo novo funkcijo:
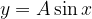
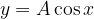
Število A je amplituda fukcije. Če je
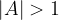 , to pomeni razteg funkcije v smeri osi y;
, to pomeni razteg funkcije v smeri osi y;
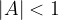 , to pomeni skrčitev funkcije v smeri osi y.
, to pomeni skrčitev funkcije v smeri osi y.
Če je A < 0, funkcijo enostavno prezrcalimo čez abscisno os.
Ko s parametrom k množimo x dosežemo razteg (ali skrčitev) kotne funkcije v smeri x osi.
Število k je frekvenca funkcije, ki nam pove število valov na dolžini ene periode 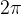 funkcije.
funkcije.
Večja ko je frekvenca, krajša je perioda. Če je
 , se funkcija raztegne v smeri osi x;
, se funkcija raztegne v smeri osi x;
 , se funkcija skrči v smeri osi x.
, se funkcija skrči v smeri osi x.
Osnovna perioda je razdalja, ki jo naredi funkcija, preden se začne ponavljati (osnovna perioda odraža natanko en obhod po enotski krožnici).
Osnovno periodo si najlažje predstavljamo na grafih:
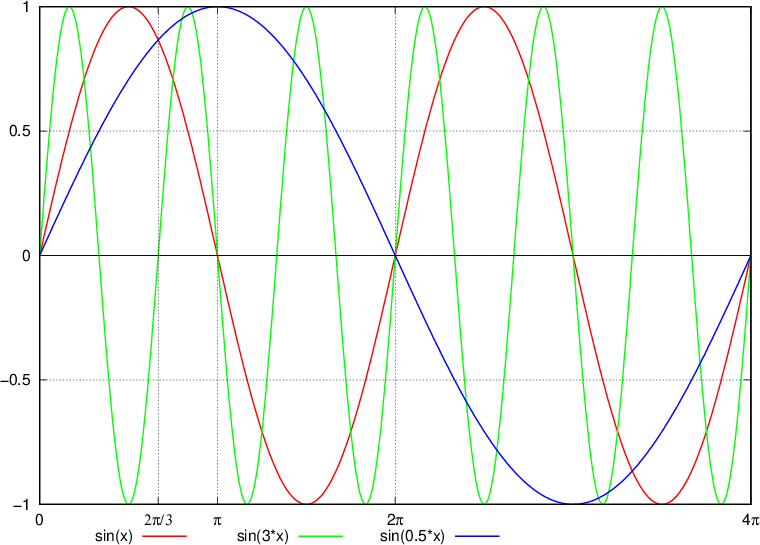
Pri prvem (rdečem) grafu preberemo, da je osnovna perioda 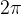 (saj se pri
(saj se pri 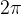 funkcija začne ponavljati).
funkcija začne ponavljati).
Pri drugem (zelenem) grafu preberemo, da je osnovna perioda 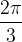 (saj se pri
(saj se pri 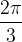 funkcija začne ponavljati).
funkcija začne ponavljati).
Pri tretjem (moderem) grafu enostavno preberemo osnovno periodo 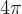 (saj se pri
(saj se pri 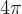 funkcija začne ponavljati).
funkcija začne ponavljati).
Zaključimo:
Osnovna perioda funkcije 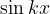 ali
ali 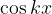 je
je
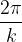
Če je:
 , je perioda manjša od
, je perioda manjša od 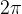
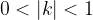 , je perioda večja od
, je perioda večja od 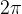
S premikom funkcije v smeri y osi, premikamo funkcijo v koordinatnem sistemu navzgor (n > 0) ali navzdol (n < 0).
S premikom funkcije v smeri x osi, premikamo funkcijo v koordinatnem sistemu levo ali desno.
Enačbi sta zapisani v najbolj splošni mogoči obliki:
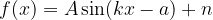
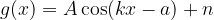
Grafe narišemo tako, da združimo vsa spoznanja prejšnjih poglavij.