Osebne zbirke


Teža ali gravitacija je sila, s katero se privlačijo mase. Deluje lahko na veliko razdaljo. Omogoča, da lahko stojimo ali hodimo po planetu Zemlja, da kroži Mesec okoli Zemlje, da se gibljejo Zemlja in ostali planeti okoli Sonca itd. Skupaj omogoča obstoj našega sončnega sistema, naše galaksije in drugih galaksij.
Vzrok gravitacije je torej masa telesa. Mase se privlačijo. Poglejmo, kako lahko izračunamo ta privlak in kakšne so njegove posledice.
Privlačno silo med dvema masama lahko izračunamo s pomočjo Newtonovega zakona gravitacije. Ta pravi, da je sila med dvema masama sorazmerna velikosti obeh mas in obratno sorazmerna kvadratu njune medsebojne razdalje:
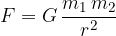
Tu sta 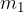 in
in 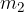 dve masi, razdalja r pa je razdalja med njunima težiščema. G je gravitacijska konstanta in znaša:
dve masi, razdalja r pa je razdalja med njunima težiščema. G je gravitacijska konstanta in znaša:
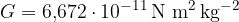
Mase se privlačijo. Privlačno silo med dvema masama izračunamo s pomočjo Newtonovega zakona gravitacije:
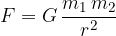
r je razdalja med težiščema obeh mas, gravitacijska konstanta G pa je:
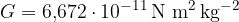
Telo z maso m stoji na površju Zemlje. Sila, ki deluje na telo, se imenuje gravitacija in smo jo spoznali v gradivu Sila in pospešek:
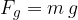
kjer je g gravitacijski ali težni pospešek. Vrednost gravitacijskega pospeška z višino pada; na površju Zemlje znaša:
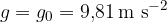
Kako pa bi ga izračunali?
Oglejmo si še enkrat Newtonov zakon gravitacije:
Gravitacijski pospešek na površju Zemlje je:
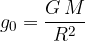
kjer je G gravitacijska konstanta, M masa Zemlje in R radij Zemlje.
Ko se dvigujemo s površja Zemlje, gravitacijski pospešek pada. Narišimo sliko!
Dvignimo se na višino h nad površje Zemlje. Naša razdalja do središča Zemlje se je povečala na:
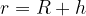
Velja Newtonov zakon gravitacije:
Dobili smo enačbo, ki določa, kako se gravitacijski pospešek spreminja z višino:
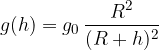
Gravitacijska sila na telo se z višino manjša:
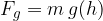
Gravitacijski pospešek v odvisnosti od višine je:
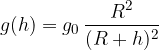
V gradivu Sile pri kroženju smo se naučili, da je vsota vseh sil, ki delujejo na telo med enakomernim kroženjem, enaka radialni sili. Pri tem predpostavimo, da kroži satelit na zadostni višini, da je upor zraka zanemarljiv.
Na satelit z maso m, ki kroži na višini h od površja Zemlje deluje samo gravitacijska sila in ta sila mora biti enaka radialni sili:
Gravitacijski pospešek je enak radialnemu pospešku. Razmislimo: če želimo, da satelit kroži okoli zemlje, drugače niti ne more biti, saj:
če bi bil gravitacijski pospešek manjši od radialnega, bi telo zbežalo v vesolje;
če bi bil gravitacijski pospešek večji od radialnega, bi telo padlo na zemljo.
Radialni pospešek izračunamo z eno od razpoložljivih enačb. Katero, je odvisno od podatkov ali veličin, ki so nam na voljo:
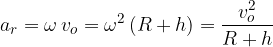
Pri tem smo upoštevali, da je razdalja od središča kroženja (R + h).
Še pred Newtonom je nemški astronom Kepler zapisal tri zakone o gibanje planetov okoli Sonca. Po njemu se zapisani zakoni imenujejo Keplerjevi zakoni.
Prvi Keplerjev zakon: planeti se gibljejo okoli Sonca po eliptičnih tirih. Sonce je v enem od gorišč elipse.
V mnogih primerih sta gorišči elipse dovolj blizu, da lahko smatramo, da se planeti gibljejo po krogu. Za radij vzamemo srednjo razdaljo planeta od Sonca.
Drugi Keplerjev zakon: zveznica med planetom in Soncem med gibanjem po eliptični tirnici v istih časovnih intervalih opiše enake ploščine (glej sliko 3).
Za lažje razumevanje zakona si narišimo skico:
Na sliki 3 smo se osredotočili na dve točki:
ko je planet najdlje od Sonca. V tej točki, skladno s sliko 3, planet v časovnem intervalu 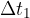 opiše ploščino
opiše ploščino 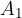 .
.
ko je planet Soncu najbližje. V tej točki, skladno s sliko 3, planet v časovnem intervalu 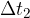 opiše ploščino
opiše ploščino 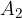 .
.
Drugi Keplerjev zakon pravi: če sta časovna intervala enaka, torej:
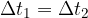
sledi, da sta opisani ploščini enaki:
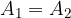
Zakon opisuje dejstvo, da se planeti, ko se po eliptičnem tiru približajo Soncu, gibljejo hitreje. Saj, če naj bosta ploščini enaki, mora biti v enakem opazovanem času dolžina poti večja od dolžine poti pri večji oddaljenosti.
Do tretjega zakona je prišel Kepler z opazovanjem. Ugotovil je, da je količnik med tretjo potenco razdalje planeta od Sonca in kvadratom obhodnega časa za vse planete enak:
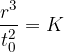
Ta količnik se imenuje Keplerjeva konstanta in znaša: