Osebne zbirke


Kinetična energija je vrsta energije, ki jo ima telo zaradi gibanja. Gibanje je lahko premo - translacijsko ali krivo gibanje. Posebna oblika krivega gibanja je kroženje ali rotacija.
V tem poglavju bomo spoznali kinetično energijo telesa pri premem gibanju telesa in pri kroženju telesa. Videli bomo, kako se spreminja energija telesa pod vplivom zunanjih sil F na poti s - torej z delom sile. Kinetično energijo označimo s črko W, ki ji dodamo indeks k:
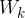
Kako telo pridobi kinetično energijo?
Telo naj najprej miruje. Po 1. Newtonovem zakonu to pomeni, da:
na njega ne deluje nobena zunanja sila ali pa
je vsota vseh sil, ki delujejo na telo, enaka nič.
V nekam trenutku prične nanj delovati sila F. V skladu z 2. Newtonovem zakonu se prične gibati enakomerno pospešeno s pospeškom a:
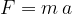
V času t naredi pot:
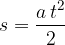
Produkt sile in poti je delo:
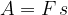
Na levi strani gornje enačbe imamo delo (A) z enoto Joule (džul) , oznaka pa 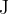 . Na desni strani pa imamo pomnoženo:
. Na desni strani pa imamo pomnoženo:
silo (F) z enoto Newton (njuten) in oznako 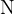 ,
,
pot (s) z enoto meter in oznako 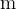 .
.
Zato lahko iz zgornje enačbe izpeljemo enoto Joule:
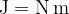
Zapišimo še enkrat enačbo:
Z delom smo torej pospešili maso m do hitrosti v. Pravimo, da smo ji dali kinetično energijo (kinematos je grška beseda za gibanje). To je le ena od oblik energij, ki jih damo telesu z delom. Ostale bomo spoznali v posebnih poglavjih.
Kinetično energijo ima vsako gibajoče se telo. Izračunamo jo po enačbi:
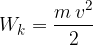
m je masa telesa.
v je hitrost telesa.
Enota za kinetično energijo je Joule (džul). Oznaka za enoto je J.
Z delom lahko spreminjamo kinetično energijo telesa.
Izrek o kinetični energiji izpeljemo s pomočjo 2. Newtonovega zakona:
Produkt 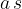 v zgornji enačbi dobimo iz enačbe za hitrost pri enakomerno pospešenem gibanju:
v zgornji enačbi dobimo iz enačbe za hitrost pri enakomerno pospešenem gibanju:
Delo je lahko pozitivno ali negativno:
Če je delo sile pozitivno - kar pomeni, da deluje sila v isto smer, kot je smer gibanja telesa - se kinetična energija veča. Telo je enakomerno pospešeno.
Če je delo negativno - sila deluje v nasprotno smer od gibanja telesa - se telesu kinetična energija manjša in telo zavira.
Izrek o kinetični energiji pravi, da je delo sile enako spremembi kinetične energije - torej končna minus začetna kinetična energija:
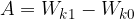
ali kratko:

Delo je lahko pozitivno ali negativno. Pozitivno delo zveča kinetično energijo telesa, negativno delo jo zmanjša.
Majhno telo z maso m (točkasto telo) kroži z obodno hitrostjo v na krožnici z radijem r. Vzeli smo majhno telo zato, da lahko predpostavimo, da se vse točke telesa gibajo z enako hitrostjo.
Tudi pri rotaciji (vrtenju, kroženju) telesa velja, da je kinetična energija:
Dobili smo izraz za rotacijsko kinetično energijo telesa.
Rotacijska kinetična energija telesa je:
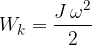
Pri tem je 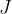 vztrajnostni moment točkastega telesa:
vztrajnostni moment točkastega telesa:
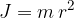
Intuitivno si lahko pojem vztrajnostnega momenta predstavljamo s primerjavo enačb za translacijsko in rotacijsko kinetično energijo:
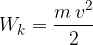
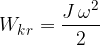
Masa m v prvi enačbi predstavlja lastnost telesa - večja kot je masa, težje premaknemo telo. Tako tudi vztrajnostni moment v drugi enačbi predstavlja lastnost telesa - večji kot je vztrajnostni moment, težje pripravimo telo k vrtenju.
Poglejmo si pojem natančneje. Začnimo s sliko:
Vztrajnostni moment sestavljenega, realnega, telesa dobimo, če seštejemo vztrajnostne momente posameznih elementarnih mas (oziroma "točkastih" teles), iz katerih je sestavljeno telo.
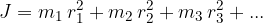
V večini primerov je izračun vztrajnostnih momentov geometrijskih teles prezapleten, da bi ga podali na tem mestu in zahteva znanje iz integriranja. Zato bomo vztrajnostne momente za nekatera najpogostejša telesa navedli kar v tabeli.
V spodnji tabeli so navedeni vztrajnostni momenti nekaterih homogenih teles, ki se vrtijo okoli simetrijske osi:
Vzemimo kroglo in valj ter ju istočasno spustimo po klancu višine h. Telesi se zakotalita po klancu navzdol. Do vznožja ne prideta istočasno. Krogla bo hitrejša od valja. Zakaj je tako?
Med kotaljenjem po klancu navzdol se bo potencialna energija pretvorila v obe vrsti kinetičnih energij, ki smo ju spoznali v tem gradivu:
kinetično energijo zaradi gibanja težišča, ki ji pravimo translacijska kinetična energija 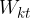 in
in
kinetično energijo zaradi vrtenja, ki ji pravimo rotacijska kinetična energija 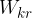 .
.
Skupna kinetična energija bo vsota obeh kinetičnih energij:
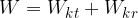
Poglejmo si obe kinetični energiji natančneje.
Vzemimo valj ali kroglo, ki se kotali po vodoravni podlagi. Kotaleče telo si predstavljajmo kot telo, ki je sestavljeno iz veliko majhnih mas 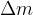 . In opazujmo eno od njih (glej spodnjo sliko). Delec se giblje po krivem tiru s hitrostjo
. In opazujmo eno od njih (glej spodnjo sliko). Delec se giblje po krivem tiru s hitrostjo 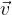 . Tir je narisan z zeleno barvo.
. Tir je narisan z zeleno barvo.
Vidimo, da hitrosti delca ni konstantna temveč se spreminja. Kako se spreminja, je odvisno od položaja opazovanega masnega delca - glej vektorje hitrosti na gornji sliki (zeleno).
V vsakem trenutku pa je hitrost poljubnega masnega delca enaka vektorski vsoti dveh hitrosti:
hitrosti gibanja težišča: 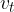
obodna hitrosti delca, ki kroži na razdalji r od težišča: 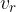
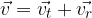
Kinetična energija izbranega delca je:
Kinetična energija 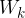 kotalečega telesa je sestavljena iz dveh delov: translacijske kinetične energije
kotalečega telesa je sestavljena iz dveh delov: translacijske kinetične energije 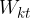 in rotacijske kinetične energije
in rotacijske kinetične energije 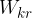 :
:
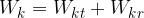
Translacijska kinetična energija je kinetična energija mase, zbrane v težišču telesa, ki se giblje s hitrostjo težišča:
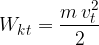
Rotacijska kinetična energija je kinetična energija, ki izhaja iz vrtenja telesa: