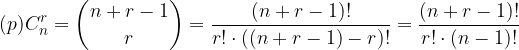Osebne zbirke


Kombinacije so razporeditve n elementov na r mest. V bistvu so to variacije, kjer zanemarimo vrstni red.
Pri kombinacijah vrstni red ni pomemben.
Kombinacije brez ponavljanja uporabimo takrat, ko želimo r elementov iz množice z n elementi razporediti na različne načine. Pri tem moramo paziti, da so ti elementi različni in se ne ponavljajo.
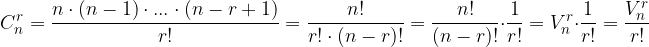
Tukaj smo sedaj dokazali, da so kombinacije v bistvu variacije, kjer zanemarimo vrstni red.
Imamo množico z n različnimi elementi in iz nje izbiramo r različnih elementov, s katerimi želimo oblikovati različne kombinacije, kjer pa vrstni red ni pomemben.
Število kombinacij brez ponavljanja tako izračunamo na naslednji način:
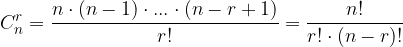
Izraz 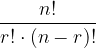 lahko zapišemo tudi z binomskim simbolom, torej:
lahko zapišemo tudi z binomskim simbolom, torej:
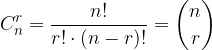
Kombinacije s ponavljanjem uporabimo takrat, ko želimo r elementov iz množice z n elementi razporediti na različne načine. Pri tem lahko isti elemnt nastopa poljubno mnogokrat.
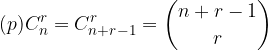
Imamo množico z n elementi in iz nje izbiramo r elementov, s katerimi želimo oblikovati različne kombinacije, kjer pa vrstni red ni pomemben in isti element lahko nastopa večkrat.
Število kombinacij s ponavljanjem tako izračunamo na naslednji način: