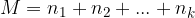Osebne zbirke


Kombinatorika je veja matematike, ki se ukvarja s preštevanjem in raziskuje število možnih razporeditev ali izborov danih elementov.
Pri osnovnem izreku kombinatorike se srečamo tudi s kombinatoričnim drevesom, ki nam grafično prikaže proces izbiranja določenih elementov.
Drevo narišemo tako, da vozlišča cepimo naprej na toliko vozlišč, kolikor možnosti imamo v danem koraku. Na koncu, ko nimamo več možnosti za cepljenje, dobimo število vseh možnih kombinacij.
Ker pa drevo lahko postane preveliko, poznamo pri kombinatoriki še drugačna pravila za računanje kombinacij.
Osnovni izrek kombinatorike ali pravilo produkta uporabimo, ko imamo na razpolago k zaporednih faz z različnim številom elementov:
v prvi fazi je možnih 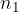 odločitev,
odločitev,
v drugi fazi je možnih 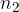 odločitev,
odločitev,
...,
v k-ti fazi pa je možnih 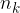 odločitev.
odločitev.
Pri tem seveda moramo upoštevati, da izbori v posamezni fazi niso odvisni od možnosti, ki so bile izbrane že v prejšnjih fazah.
Če najprej izbiramo med 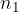 odločitvami, potem neodvisno od prvega izbora, izbiramo med
odločitvami, potem neodvisno od prvega izbora, izbiramo med 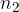 odločitvami, ... in nazadnje neodvisno od prejšnjega izbora, izbiramo med
odločitvami, ... in nazadnje neodvisno od prejšnjega izbora, izbiramo med 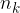 odločitvami, potem je število vseh izborov (N) enako produktu vseh odločitev (
odločitvami, potem je število vseh izborov (N) enako produktu vseh odločitev (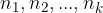 ) v posamezni fazi:
) v posamezni fazi:
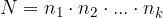
Govori o situaciji, ko imamo na razpolago dve ali več množic, ki nimajo skupnega preseka, in izbiramo med elementi ene izmed vseh množic.
Pravilo vsote torej pride v poštev, ko izbiramo med:
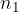 možnostmi iz prve množice izborov
možnostmi iz prve množice izborov
ali
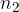 možnostmi iz druge množice izborov
možnostmi iz druge množice izborov
ali
...
ali
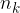 možnostmi iz k-te množice izborov
možnostmi iz k-te množice izborov
Izbori iz vsake množice so nezdružljivi z izbori iz drugih množic. Izberemo lahko element iz prve ali druge množice, nikoli iz obeh hkrati.
Če se pri izbiranju odločimo ali za eno od 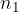 možnosti iz prve množice ali za eno od
možnosti iz prve množice ali za eno od 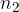 možnosti iz druge množice ... ali za eno od
možnosti iz druge množice ... ali za eno od 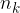 možnosti, dobimo število vseh izborov (M), ki je enako vsoti elementov (
možnosti, dobimo število vseh izborov (M), ki je enako vsoti elementov (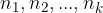 ) iz posameznih množic:
) iz posameznih množic: