Prijava z e-naslovom
Prijava brez gesla
V vsakem koraku konstrukcije geometrijskega lika narišemo enega izmed osnovnih geometrijskih elementov:
Točko prostoročno narišemo kot piko, premico pa narišemo z ravnilom kot neskončno ravno črto (pri tem smo seveda omejeni z robovi lista):
Točka A in premica p
Premico lahko potegnemo skozi točko:
Premica p poteka skozi točko A
Točka A razdeli premico p na dva poltraka. Premica p predstavlja nosilko teh dveh poltrakov:
Poltraka h in k s skupnim izhodiščem A
Krožnico konstruiramo na podlagi poznavanja konstrukcije točke. Edini podatek, ki ga potrebujemo za konstruiranje krožnice, je njen polmer.
1. korak
Prostoročno narišemo točko S. Točka S predstavlja središče krožnice.
2. korak
Krožnico narišemo s šestilom:
V šestilo vzamemo polmer krožnice r.
Šestilo zapičimo v točko S.
Zarišemo sklenjeno krivo črto okoli točke S:
Daljico konstruiramo na podlagi poznavanja konstrukcije točke in premice.
Edini podatek, ki ga potrebujemo za konstruiranje daljice, je njena dolžina.
1. korak
Prostoročno narišemo točko A in skoznjo z ravnilom potegnemo premico p. Točka A predstavlja prvo krajišče daljice:
2. korak
S šestilom začrtamo drugo krajišče daljice:
V šestilo vzamemo dolžino daljice d.
Šestilo zapičimo v točko A.
S šestilom zarišemo krožni lok tako, da seka premico p:
3. korak
Presečišče premice in krožnega loka označimo s točko B. Točka B predstavlja drugo krajišče daljice:
Konstruirali smo daljico AB oziroma njej enakovredno daljico BA. Premica p predstavlja nosilko konstruirane daljice.
Simetralo daljice konstruiramo na podlagi poznavanja konstrukcije krožnice in premice.
Preden se lotimo risanja, ponovimo definicijo simetrale daljice:
Simetrala daljice je premica, ki razpolavlja daljico in je pravokotna nanjo.
Predpostavimo, da je daljica AB že narisana:
1. korak
V šestilo vzamemo dolžino, nekoliko večjo od polovične dolžine daljice AB.
Šestilo zapičimo v točko A.
S šestilom zarišemo krožni lok tako, da seka daljico AB:
2. korak
Položaja krakov šestila ne spreminjamo.
Šestilo zapičimo v točko B.
S šestilom zarišemo tak krožni lok, ki seka daljico AB, obenem pa dvakrat seka predhodno narisan krožni lok.
Točki, v katerih se krožna loka sekata, označimo s točkama C in D:
3. korak
Z ravnilom narišemo premico skozi točki C in D ter jo označimo z malo črko s:
Premica skozi točki C in D je simetrala daljice AB in je na daljico AB pravokotna.
4. korak
Presečišče daljice AB in njene simetrale označimo s točko E:
Točka E predstavlja razpolovišče daljice AB. Simetrala s torej razpolavlja daljico AB.
Pravokotnico konstruiramo na podlagi poznavanja konstrukcije krožnice in premice.
Preden se lotimo risanja, ponovimo definicijo pravokotnice:
Pravokotnica je premica, ki z dano daljico oz. premico oklepa pravi kot.
Predpostavimo, da sta premica p in točka T, skozi katero želimo potegniti pravokotnico, že narisani:
1. korak
V šestilo vzamemo poljubno dolžino.
Šestilo zapičimo v točko T.
S šestilom zarišemo krožnico.
Presečišči krožnice in premice označimo s točkama A in B:
2. korak
V šestilo vzamemo dolžino, nekoliko večjo od polovične dolžine daljice AB.
Šestilo zapičimo v točko A.
S šestilom zarišemo krožni lok v področje nad premico p:
3. korak
Položaja krakov šestila ne spreminjamo.
Šestilo zapičimo v točko B.
S šestilom zarišemo krožni lok tako, da seka krožnico s središčem v točki A.
Tako nastalo presečišče označimo s točko C:
4. korak
Z ravnilom narišemo premico skozi točki T in C ter jo označimo s q:
Premica q je pravokotnica na premico p:
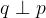
Predpostavimo, da sta premica p in točka T, skozi katero želimo potegniti pravokotnico, že narisani:
1. korak
V šestilo vzamemo dolžino, nekoliko večjo od razdalje med točko in premico.
Šestilo zapičimo v točko T.
S šestilom zarišemo krožni lok tako, da dvakrat seka premico p.
Presečišči krožnega loka in premice označimo s točkama A in B.
2. korak
V šestilo vzamemo dolžino, nekoliko večjo od polovične dolžine daljice AB.
Šestilo zapičimo v točko A.
S šestilom zarišemo krožni lok tako, da seka daljico AB:
3. korak
Položaja krakov šestila ne spreminjamo.
Šestilo zapičimo v točko B.
S šestilom zarišemo tak krožni lok, ki seka daljico AB, obenem pa seka tudi predhodno narisan krožni lok.
Točki, v katerih se krožna loka sekata, označimo s točkama C in D:
4. korak
Z ravnilom narišemo premico skozi točki C in D in jo označimo s q:
Premica q je pravokotnica na premico p:
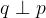
Vzporednico konstruiramo na podlagi poznavanja konstrukcije krožnice, premice in pravokotnice.
Preden se lotimo risanja, ponovimo definicijo vzporednice:
Vzporednica je premica, ki z dano daljico oz. premico bodisi nima nobene skupne točke bodisi sovpada.
Predpostavimo, da sta premica p in točka T, skozi katero želimo potegniti vzporednico, že narisani:
1. korak
Na premici p označimo poljubno točko A.
V šestilo vzamemo razdaljo med točkama A in T.
Šestilo zapičimo v točko A.
S šestilom zarišemo krožni lok tako, da seka premico p in hkrati poteka skozi točko T.
Tako nastalo presečišče premice in krožnega loka označimo s točko B:
2. korak
Položaja krakov šestila ne spreminjamo.
Šestilo zapičimo v točko T.
S šestilom zarišemo krožni lok tako, da ne seka predhodno narisanega krožnega loka:
3. korak
Položaja krakov šestila ne spreminjamo.
Šestilo zapičimo v točko B.
S šestilom zarišemo krožni lok tako, da seka krožnico s središčem v točki T.
Tako nastalo presečišče označimo s točko C:
4. korak
Z ravnilom narišemo premico skozi točki T in C ter jo označimo s q:
Premica q je vzporednica k premici p:
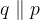
Predpostavimo, da je premica p, ob kateri želimo potegniti vzporednico, že narisana:
1. korak
Na premici p označimo poljubno točko A:
2. korak
Konstruiramo pravokotnico na premico p skozi točko A in jo označimo s q:
3. korak
V šestilo vzamemo podano razdaljo med premico p in njeno vzporednico.
Šestilo zapičimo v točko A.
S šestilom zarišemo krožnico.
Presečišči krožnice in premice q označimo s točkama B in C:
4. korak
Konstruiramo pravokotnico na premico q skozi točko B in jo označimo z r:
Konstruiramo pravokotnico na premico q skozi točko C in jo označimo z s:
Premici r in s sta vzporednici k premici p na razdalji d:
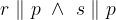
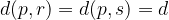
Tovrstna konstrukcija ima vedno dve rešitvi, zato lahko zapišemo:
Vsaki premici v ravnini pripadata dve vzporednici, ki sta od premice enako oddaljeni.
Simetralo kota konstruiramo na podlagi poznavanja konstrukcije krožnice in premice.
Preden se lotimo risanja, ponovimo definicijo simetrale kota:
Simetrala kota je premica, ki poteka skozi vrh kota in razpolavlja kot.
Predpostavimo, da je ravninski kot z vrhom V že narisan:
1. korak
V šestilo vzamemo poljubno dolžino.
Šestilo zapičimo v točko V.
S šestilom zarišemo krožni lok tako, da seka oba kraka kota.
Točki, v katerih krožni lok seka kraka kota, označimo z A in B:
2. korak
Položaja krakov šestila ne spreminjamo.
Šestilo zapičimo v točko A.
S šestilom zarišemo krožni lok v področje med krakoma kota:
3. korak
Položaja krakov šestila ne spreminjamo.
Šestilo zapičimo v točko B.
S šestilom zarišemo krožni lok v področje med krakoma kota tako, da seka predhodno zarisan krožni lok.
Točko, v katerih se krožna loka sekata, označimo s C:
4. korak
Z ravnilom narišemo premico skozi točki V in C:
Premica skozi točki V in C je simetrala kota AVB.
Kot 60° konstruiramo na podlagi poznavanja konstrukcije krožnice in premice.
1. korak
Prostoročno narišemo točko V.
Z ravnilom skozi točko V potegnemo premico p:
2. korak
V šestilo vzamemo poljubno dolžino.
Šestilo zapičimo v točko V.
S šestilom zarišemo krožni lok tako, da seka premico p. Krožni lok naj se nahaja pretežno nad premico p.
Tako nastalo presečišče označimo s točko A:
3. korak
Položaja krakov šestila ne spreminjamo.
Šestilo zapičimo v točko A.
S šestilom zarišemo krožni lok v področje nad premico tako, da seka predhodno zarisan krožni lok.
Presečišče krožnih lokov označimo s točko B:
4. korak
Z ravnilom narišemo poltrak, ki ima izhodišče v točki V in poteka skozi točko B:
Konstruirali smo kot AVB, ki meri 60°.
5. korak (dodatni korak)
Z ravnilom povežemo točki A in B:
Posredno smo poleg 
AVB konstruirali še dva kota 60° in sicer BAV ter VAB. Tako konstruirani koti so notranji koti enakostraničnega trikotnika z oglišči V, A in B.
Konstrukcija kota 60° temelji na dejstvu, da so notranji koti v enakostraničnem trikotniku skladni in merijo 60°.
Konstrukcije enakostraničnih (pravilnih) likov so podrobneje predstavljene v poglavju Konstruiranje pravilnih geometrijskih likov
Tangento konstruiramo na podlagi poznavanja konstrukcij:
krožnice
premice
razpolovišča daljice in
pravokotnice
Potrebno pa je tudi poznavanje Talesovega izreka o kotu v polkrogu.
Preden se lotimo risanja, ponovimo definicijo tangente:
Tangenta je premica, ki se dotika krožnice v natanko eni točki in je pravokotna na polmer krožnice.
Predpostavimo, da sta krožnica in točka T, skozi katero želimo potegniti tangento, že narisani:
1. korak
Z ravnilom narišemo poltrak, ki ima izhodišče v središču krožnice S in poteka skozi točko T. Poltrak označimo s h:
2. korak
Konstruiramo pravokotnico na poltrak h skozi točko T in jo označimo s t:
Premica t predstavlja tangento na krožnico s središčem v točki S.
Predpostavimo, da sta krožnica in točka T, skozi katero želimo potegniti tangento, že narisani:
1. korak
Z ravnilom povežemo točki S in T:
2. korak
Konstruiramo razpolovišče daljice ST in ga označimo s točko A:
3. korak
V šestilo vzamemo polovično dolžino daljice ST.
Šestilo zapičimo v točko A.
S šestilom zarišemo krožnico.
Presečišči krožnic označimo s točkama B in C:
4. korak
Z ravnilom narišemo premico skozi točki T in B in jo označimo s t.
Z ravnilom narišemo premico skozi točki T in C in jo označimo z u:
Središčni kot TAS v krogu s središčem A (na zgornji sliki označen zeleno) meri 180°.
Glede na izrek o središčnem in obodnem kotu je pripadajoči obodni kot TBS za polovico manjši, t.j. pravi kot.
Enako velja za kota TAS in TCS - tudi slednji je pravi kot.
Premici t in u torej predstavljata tangenti na krožnico s središčem v točki S.
Tovrstna konstrukcija ima vedno dve rešitvi, zato lahko zapišemo:
Skozi točko izven krožnice vedno lahko narišemo dve tangenti na krožnico.
