Osebne zbirke


Krog opišemo s središčem (točka S) in polmerom (razdalja r) oziroma premerom (razdalja d, ki je dvakratnik polmera). Središče določa položaj kroga v ravnini, polmer pa njegovo velikost.
Krožnica je vase zaključena krivulja, ki je v vsaki točki od središča oddaljena natanko za polmer:
Če k krožnici prištejemo še površino znotraj krožnice, dobimo krog:
Ne pozabimo, da krog vsebuje tudi krožnico!
Definirajmo do sedaj obravnavane pojme:
Krog je množica vseh točk v ravnini, katerih razdalja do središča kroga je manjša ali enaka polmeru kroga.
Krožnica je množica točk v ravnini, katerih razdalja do središča kroga je enaka polmeru kroga.
Središče je točka, ki se nahaja v sredini kroga in je enako oddaljena od vseh točk krožnice. Označimo jo z veliko tiskano črko S.
Polmer je razdalja od središča do katere koli točke na krožnici. Označimo ga z malo tiskano črko r.
Premer je največja razdalja med dvema točkama na krožnici. Označimo ga z malo tiskano črko d.
Enačba za obseg kroga se glasi:
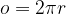
Enačba za ploščino kroga se glasi:
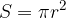
Naj bo l krožni lok s krajišči v točkah A in B, k pa dopolnilni lok loka l.
Središčni kot nad lokom l ima vrh v središču krožnice, njegova kraka pa krožnico sekata v krajiščih loka.
Obodni kot nad lokom l ima vrh v točki C na loku k, njegova kraka pa krožnico sekata v krajiščih loka:
Izrek o središčnem in obodnem kotu se glasi:
Središčni kot meri dvakratno vrednost obodnega kota nad istim lokom:
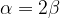
Naj bo daljica AB premer kroga. Krožni lok AB in njegov dopolnilni lok predstavljata polkrožnici.
Če vrh kota 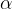 leži na polkrožnici, kraka pa potekata skozi krajišči premera, potem je
leži na polkrožnici, kraka pa potekata skozi krajišči premera, potem je 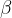 pravi kot:
pravi kot:
Krožni lok je del krožnice, omejen z dvema točkama.
Krožna loka z istimi krajišči imenujemo dopolnilna loka.
Dopolnilna loka skupaj sestavljata celotno krožnico (na sliki sta označena z l in k):
Krožni lok, katerega krajišči sta enaki krajiščema premera, imenujemo polkrožnica.
Razmerje dolžine krožnega loka in celotnega obsega kroga je enako razmerju velikosti središčnega kota in polnega kota:
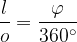
Ob upoštevanju enačbe za obseg kroga tako lahko zapišemo
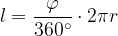
Tetiva je daljica, ki povezuje dve točki na krožnici. Najdaljša tetiva je premer.
Krožni izsek je množica točk, omejena s krožnim lokom in polmeroma do krajišč krožnega loka:
Razmerje ploščine krožnega izseka in ploščine celotnega kroga je enako razmerju velikosti središčnega kota in polnega kota:
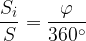
Ob upoštevanju enačbe za ploščino kroga tako lahko zapišemo
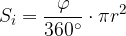
Krožni odsek je množica točk, omejena s krožnim lokom in tetivo med krajišči krožnega loka:
Ploščino krožnega odseka dobimo tako, da ploščino krožnega izseka nad središčnim kotom 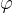 zmanjšamo za ploščino enakokrakega trikotnika ABS (glej zgornjo sliko), katerega kraka sta enaka polmeru kroga, njegova osnovnica pa je tetiva med krajišči krožnega loka nad središčnim kotom
zmanjšamo za ploščino enakokrakega trikotnika ABS (glej zgornjo sliko), katerega kraka sta enaka polmeru kroga, njegova osnovnica pa je tetiva med krajišči krožnega loka nad središčnim kotom 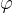 :
:
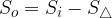
Ob upoštevanju enačbe za ploščino krožnega izseka in ploščino enakokrakega trikotnika tako lahko zapišemo
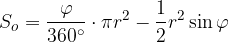
Zgornja enačba velja ob predpostavki, da je središčni kot manjši od 180°:
Izpeljavo enačbe za ploščino enakokrakega trikotnika ABS si lahko ogledate v poglavju Pravilni n-kotnik.
Krožni kolobar je množica točk med dvema krožnicama s skupnim središčem in različnima polmeroma.
Polmera sta na sliki označena z 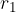 in
in 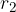 :
:
Ploščino krožnega kolobarja dobimo tako, da ploščino manjšega (notranjega) kroga odštejemo od ploščine večjega kroga:
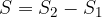
Ob upoštevanju enačbe za ploščino kroga tako lahko zapišemo
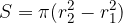
Premica krožnico lahko seka, lahko se je dotika ali teče mimo nje:
Sekanta je premica, ki seka krožnico v dveh točkah. Sekanta je nosilka tetive.
Tangenta je premica, ki se dotika krožnice v natanko eni točki. Tangenta je pravokotna na polmer.
Mimobežnica je premica, ki s krožnico nima nobene skupne točke.
Trikotniku lahko očrtamo krožnico. Pri tem si pomagamo s simetralo daljice. Vsaka stranica trikotnika je daljica in ji lahko narišemo simetralo. Za simetralo daljice je značilno, da je vsaka točka na njej enako oddaljena od obeh krajišč daljice, v našem primeru sta to dve oglišči trikotnika. Če želimo trikotniku očrtati krožnico, moramo najti točko, ki bo enako oddaljena od vseh treh oglišč trikotnika. To naredimo tako, da vsaki od stranic trikotnika narišemo simetralo:
Točka, v kateri se sekajo simetrale stranic, predstavlja središče trikotniku očrtane krožnice. Oglišča trikotnika so od te točke oddaljene ravno za polmer, zato skoznje lahko izrišemo krožnico.
Trikotniku krožnico lahko tudi včrtamo. Pri tem si pomagamo s simetralo kota. Trikotnik ima tri kote in vsakemu od njih lahko vrišemo simetralo. Za simetralo kota je značilno, da je vsaka točka na njej enako oddaljena od nosilk krakov kota, v našem primeru sta to stranici trikotnika, ki oklepata kot. Če želimo trikotniku očrtati krožnico, moramo najti točko, ki bo enako oddaljena od vseh treh stranic. To naredimo tako, da vsakemu od kotov trikotnika narišemo simetralo.
Točka, v kateri se sekajo simetrale kotov, predstavlja središče trikotniku včrtane krožnice. Stranice trikotnika so od te točke oddaljene ravno za polmer, zato bo imela včrtana krožnica z vsako od njih natanko eno skupno točko.
Krožnico lahko očrtamo tetivnemu štirikotniku:
Tetivni štirikotnik ima nasprotna kota suplementarna:
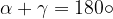
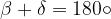
Krožnico lahko včrtamo tangentnemu štirikotniku:
V tangentnem štirikotniku je vsota dolžin dveh nasprotnih stranic enaka vsoti dolžin drugih dveh nasprotnih stranic:
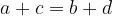
Krožnico lahko tako očrtamo kot tudi včrtamo vsakemu pravilnemu n-kotniku.
Spodnja slika prikazuje primer za pravilni 6-kotnik. Z rdečo barvo je narisana očrtana, z modro pa včrtana krožnica: