Osebne zbirke
Prijava z e-naslovom
Prijava brez gesla
Krožne (ciklometrične) funkcije so kotnim funkcijam (sinus, kosinus in tangens, kotangens) obratne ali inverzne funkcije. Imenujemo jih tudi arkus funkcije.
Najbolj uporabljene arkus funkcije in njihove oznake:
arkus sinus: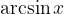 
arkus kosinus: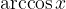 
arkus tangens: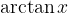 
Grafi inverznih funkcij so zrcalne slike monotonega intervala grafov funkcij glede na simetralo lihih kvadrantov.
Vrednost kota x na vseh grafih inverznih funkcij se izraža v radianih. To pomeni, da je vrednost π enaka 3.14159... in ne 180°.
Za vsak
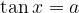
velja, da
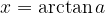
Funkcija arkus tangens
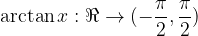
je inverzna (obratna) funkcija k funkciji tangens
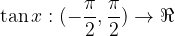
Oba grafa v nadaljevanju prikazujeta arctan x, ki ga dobimo tako, da monotono vejo tangensa z intervala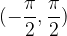 
prezrcalimo prek simetrale lihih kvadrantov.
Ena veja arctan x:
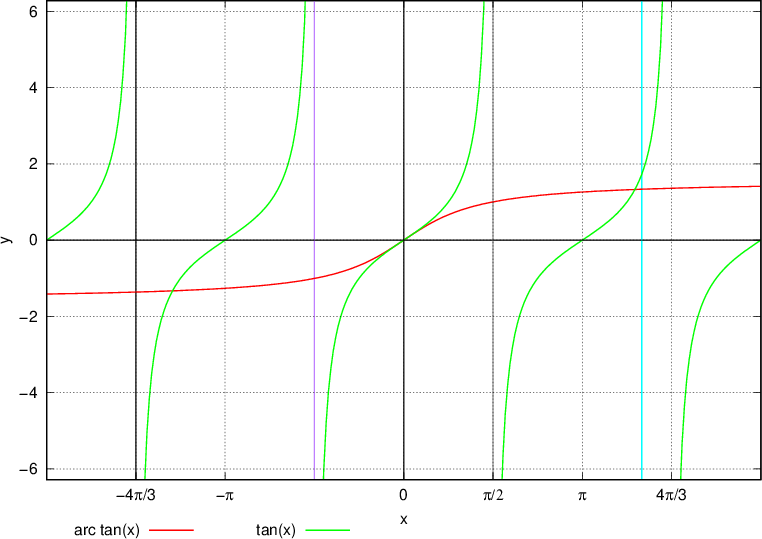
Celoten arctan x:
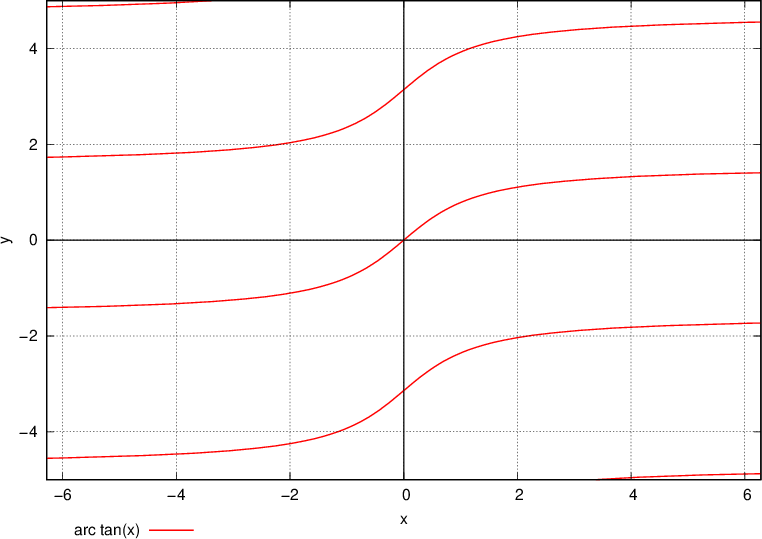
Definicijsko območje funkcije arkus tangens je množica vseh realnih števil.
Zaloga vrednosti arkus tangens je interval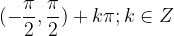 
.
Funkcija arkus tangens je na celem definicijskem območju naraščajoča.
Velja: funkciji arkus tangens in tangens se medsebojno ''uničujeta'', kar zapišemo:
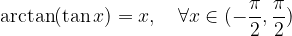
in
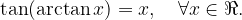
Enačba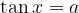 
ima vedno neskončno mnogo realnih rešitev. Po dogovoru je rezultat funkcije arkus tangens po absolutni vrednosti najmanjša rešitev enačbe.
Na grafu preberemo rešitve:
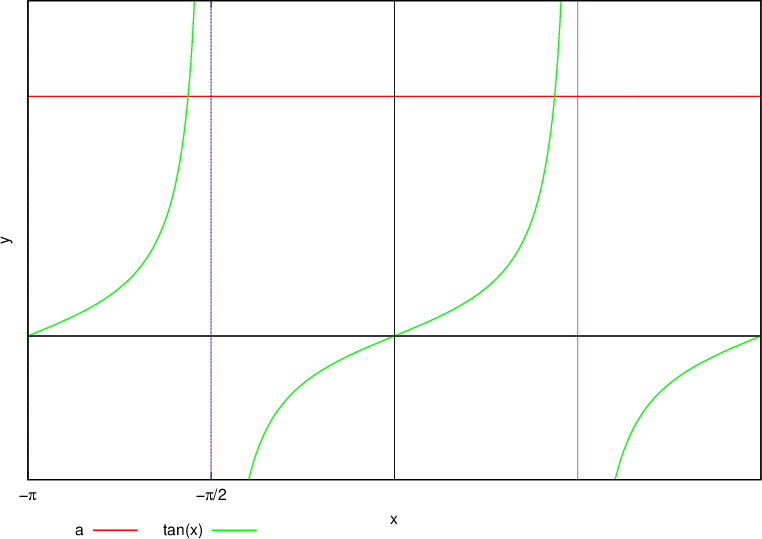
Rešitve dobimo tako, da v kalkulator vtipkamo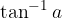 
in upoštevamo periodičnost funkcije.
Vse rešitve enačbe zapišemo:
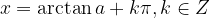
Za vsak
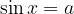
velja, da
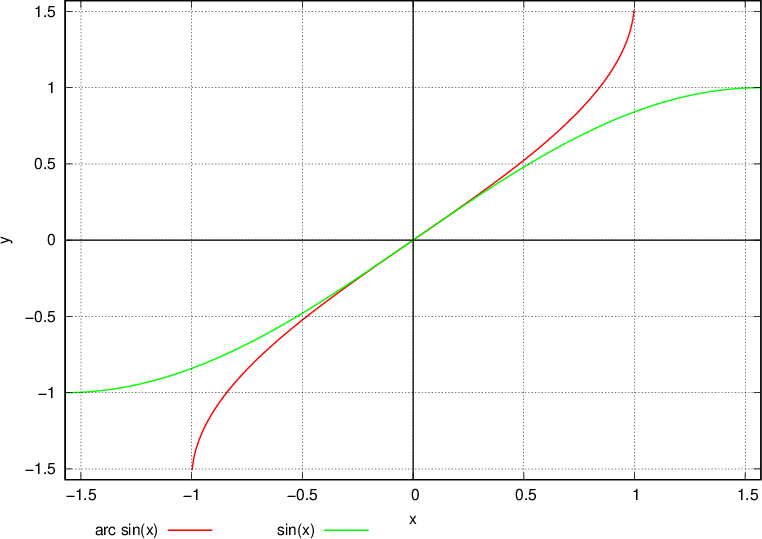
Funkcija arkus sinus
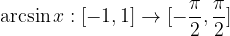
je inverzna (obratna) funkcija funkcije sinus
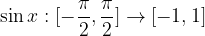
Graf arcsin x dobimo tako, da vzamemo monotoni del sinusa z intervala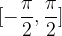 
in ga prezrcalimo preko simetrale lihih kvadrantov.
Definicijsko območje arkus sinus funkcije je interval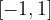 
.
Zaloga vrednosti arkus sinus funkcije je interval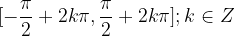 
.
Funkcija je naraščajoča na celotnem definicijskem območju.
Velja: funkciji arkus sinus in sinus se medsebojno ''uničujeta'', kar zapišemo:
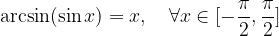
in
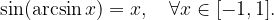
Če je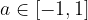 
, potem ima enačba 
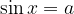neskončno mnogo realnih rešitev. Po dogovoru je rezultat funkcije arkus sinus po absolutni vrednosti najmanjša rešitev enačbe .
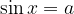Rešitve lahko preberemo na dva načina:
Reševanje s pomočjo grafa
Pri reševanju z grafom gledamo presečišče funkcij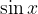 
in 
.
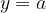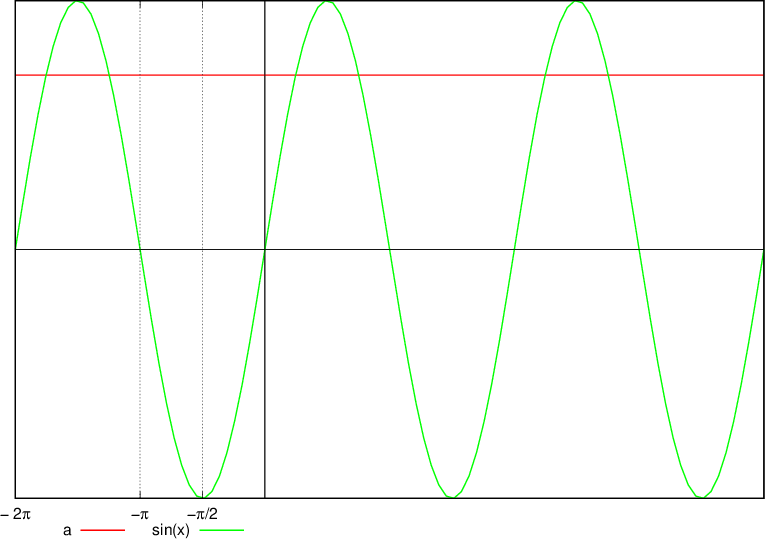
Reševanje s pomočjo enotske krožnice
v enotski krožnici
Ne glede na način reševanja so rešitve vedno enake:
prvi sklop rešitev dobimo s kalkulatorjem (vtipkamo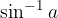 
)
drugi sklop rešitev pa tako, da prvo rešitev odštejemo od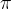 
-ja
V obeh primerih upoštevamo periodičnost funkcije.
Rešitve enačbe :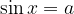
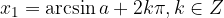
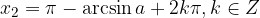
Če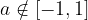 
, potem enačba 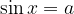nima realnih rešitev.
Za vsak
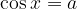
velja, da
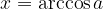
Funkcija arkus kosinus
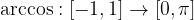
je inverzna (obratna) funkcija funkcije kosinus:
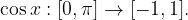
Graf arccos x dobimo tako, da vzamemo monotoni del kosinusa z intervala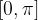 
in ga prezrcalimo preko simetrale lihih kvadrantov.
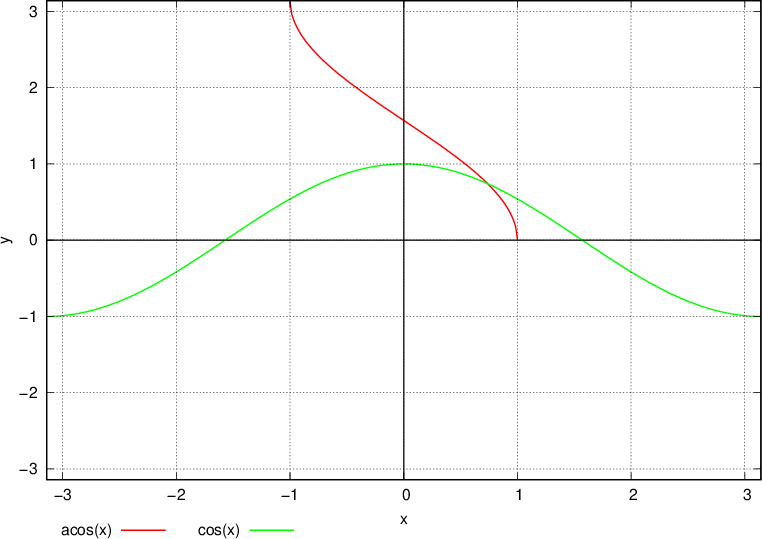
Definicijsko območje funkcije arkus kosinus je interval .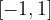
Zaloga vrednosti funkcije je interval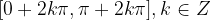 
.
Funkcija je padajoča na celotnem definicijskem območju.
Velja: funkciji arkus kosinus in kosinus se medsebojno ''uničujeta'', kar zapišemo:
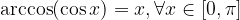
in
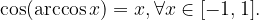
Če je 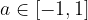, potem ima enačba 
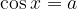neskončno mnogo realnih rešitev. Po dogovoru je rezultat funkcije arkus kosinus najmanjša nenegativna rešitev enačbe 
.
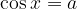Rešitve lahko preberemo na dva načina:
Reševanje s pomočjo grafa:
Pri reševanju z grafom gledamo presečišče funkcij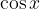 
in .
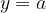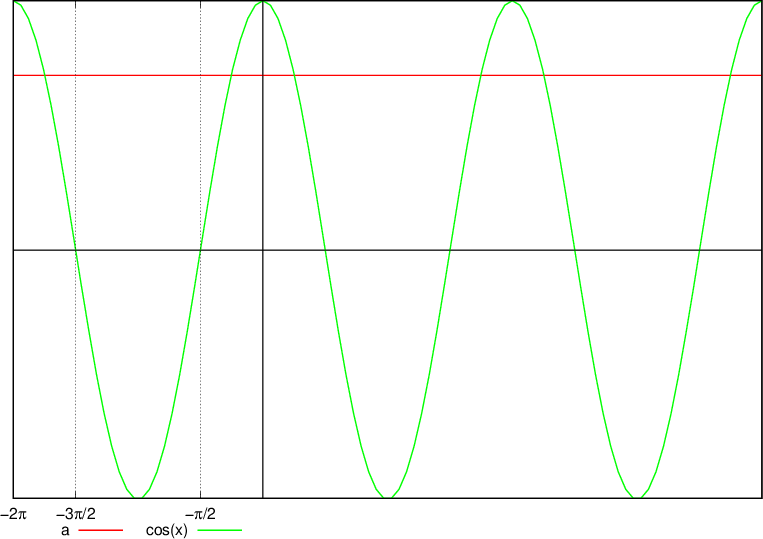
Reševanje s pomočjo enotske krožnice:
v enotski krožnici
Ne glede na način reševanja dobimo iste rezultate.
prvi sklop rešitev dobimo s kalkulatorjem (vtipkamo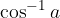 
)
drugi sklop rešitev pa tako, da prvo rešitev nasprotno predznačimo
V obeh primerih upoštevamo periodičnost funkcije.
Vse rešitve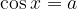
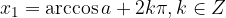
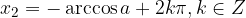
Če 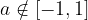, potem enačba 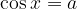nima realnih rešitev.
