Osebne zbirke


Okolica točke 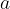 na številski premici je odprt interval s središčem v
na številski premici je odprt interval s središčem v 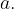
Če sta meji intervala oddaljeni od točke 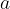 za
za 
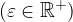 , potem ta interval širine
, potem ta interval širine 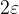 zapišemo:
zapišemo: 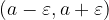 in ga imenujemo
in ga imenujemo  - okolica točke
- okolica točke 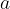 . Označimo jo:
. Označimo jo:
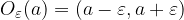
Okolica je lahko poljubno velik interval, širina intervala je odvisna od izbire pozitivnega števila  (ki pa je ponavadi, ko želimo kaj dokazati, zelo majhen).
(ki pa je ponavadi, ko želimo kaj dokazati, zelo majhen).
Število 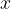 je v
je v  - okolici točke
- okolici točke 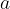 , če je od točke
, če je od točke 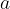 oddaljeno za manj kot
oddaljeno za manj kot 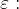

Okolico točke 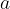 torej lahko zapišemo kot množico vseh takih realnih števil
torej lahko zapišemo kot množico vseh takih realnih števil 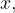 ki so od
ki so od 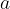 oddaljena za manj kot
oddaljena za manj kot 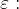
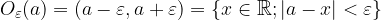
Kdaj v dani točki 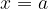 limita funkcije
limita funkcije 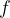 obstaja?
obstaja?
Izberimo si poljubno majhno pozitivno realno število  , ki določa okolico točke
, ki določa okolico točke 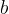 na ordinatni osi. Preverimo, ali k izbranemu
na ordinatni osi. Preverimo, ali k izbranemu  obstaja tako pozitivno realno število
obstaja tako pozitivno realno število 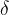 , da vse vrednosti
, da vse vrednosti 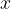 iz
iz 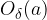 na abscisni osi (razen morda točke
na abscisni osi (razen morda točke 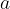 ) preslikajo v
) preslikajo v 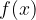 iz
iz 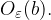
Če obstaja, potem pravimo, da limita funkcije 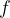 v točki
v točki 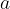 obstaja in je enaka
obstaja in je enaka 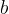 . Pri tem ni pomembno, ali je funkcija v točki
. Pri tem ni pomembno, ali je funkcija v točki 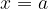 definirana ali ne.
definirana ali ne.
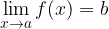 , če za vsak
, če za vsak 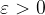 obstaja tak
obstaja tak 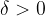 , da velja:
, da velja:
če je 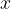 v
v 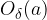 in
in 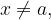 je tudi
je tudi 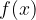 v
v 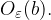
Oziroma:
Limita
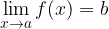
obstaja, če za vsak 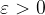 obstaja tak
obstaja tak 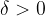 , da velja:
, da velja:
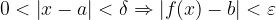
Pri definiciji limite funkcije je pomembno, da k vsakemu še tako majhnemu  lahko najdemo ustrezen
lahko najdemo ustrezen 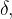 sicer limita v točki
sicer limita v točki 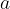 ne obstaja.
ne obstaja.
Za računanje z limitami (če seveda obstajajo limite posameznih funkcij v  ) veljajo naslednja pravila:
) veljajo naslednja pravila:
1. Limita vsote je enaka vsoti limit:
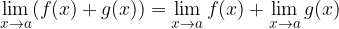
2. Limita produkta konstantnega faktorja in funkcije je enaka limiti funkcije, pomnožene s konstanto:
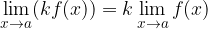
3. Limita produkta je enaka produktu limit:
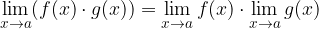
4. Limita kvocienta je enaka kvocientu limit, če je limita v imenovalcu različna od nič: