Osebne zbirke
Prijava z e-naslovom
Prijava brez gesla
V tem poglavju bomo obravnavali limite naslednjih trigonometričnih funkcij:
V nadaljevanju si bomo pogledali dva tipa limit:
limito v neki točki (npr. v točki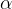 
)
limito v neskončnosti.
Spomnimo se kakšen graf imata funkciji sinus in kosinus.
Vemo, da ima limita funkcije v točki 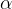naslednjo obliko:
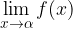
S pomočjo grafa opazimo, da sta sinus in kosinus zvezni funkciji na vsem definicijskem območju, zato za njuni limiti velja:
Limita funkcije sinus v točki:
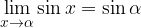
Limita funkcije kosinus v točki:
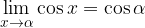
Posebej zanimiva je naslednja limita:
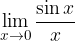
Problem limite je, da če v izraz vstavimo x=0, dobimo:
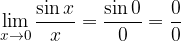
Odvisno od tega, kako hitro funkciji v števcu in imenovalcu padajo proti ničli, je lahko vrednost takega izraza karkoli med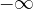 
in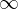 
.
Kljub temu limita v x=0 obstaja in sicer:
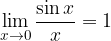
Dokažimo enakost; pri tem si pomagamo s skico:
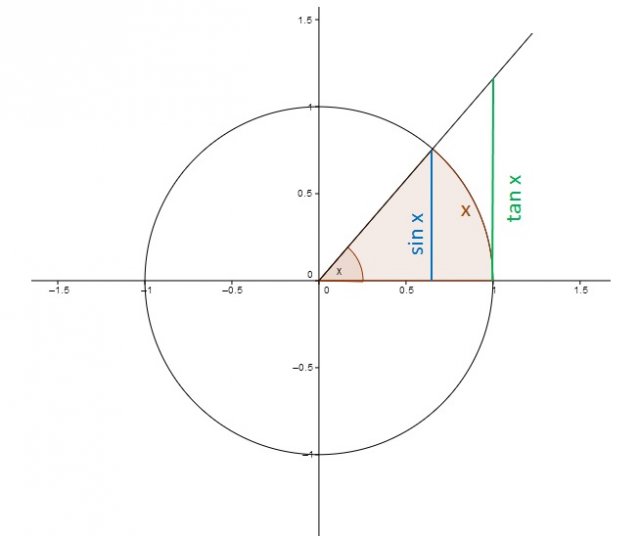
V enotsko krožnico smo vrisali kot x (v radianih). Ker smo v enotski krožnici, je lok, ki pripada temu kotu, dolžine x. Označimo še razdalji x in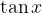 
.
Iz skice lahko, na intervalu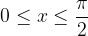 
, zapišemo očitno zvezo:
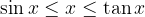
Oglejmo si zvezo podrobneje:
Opomba:
Ta primer oz. trditev je lahko tudi zelo uporabna pri drugih problemih, zato ga bomo označili kot zgoraj dokazano trditev:
Limita funkcije
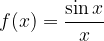
v točki x=0 je enaka 1
Torej:
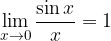
Vemo, da ima limita funkcije v neskončnosti naslednjo obliko:
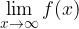
Vemo tudi, da se vrednosti funkcije sinus in kosinus gibljejo med -1 in 1, zato lahko trdimo naslednje:
O limiti funkcije sinus in kosinus v neskončnosti ne moremo govoriti, ker se njune vrednosti vedno gibljejo med -1 in 1 in se ne približujejo nobeni vrednosti. Limiti
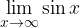
in
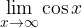
ne obstajata.
Spomnimo se grafa funkcije tanges in kotanges. S pomočjo tega ugotovimo naslednje:
Tanges in kotanges sta odsekoma zvezni funkciji. Zanju velja naslednje:
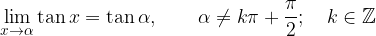
Vrednost
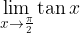
ne obstaja, saj gredo vrednosti funkcije tanges, ko se x približuje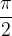 
z leve, v plus neskončno, ko se x približuje vrednosti 
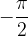z desne, v minus neskončno. Podoben sklep naredimo za funkcijo kotanges za vrednost 
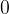in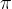 
.
