Osebne zbirke


Linearna funkcija je funkcija, katere graf v koordinatnem sistemu je ravna črta oziroma premica. Ime linearne funkcije namreč izhaja iz latinske besede linea, ki v prevodu pomeni "ravna črta".
Linearna funkcija je izmed vseh funkcij najbolj preprosta, kar se odraža tudi na njenem grafu - neskončni ravni črti.
Poseben primer linearne funkcije je premo sorazmerje. Graf premega sorazmerja vedno poteka skozi koordinatno izhodišče.
Predpis funkcije je enačba, ki opisuje odvisnost med spremenljivkama  in
in  :
:
Spremenljivka  je odvisna od spremenljivke
je odvisna od spremenljivke  . To pomeni, da
. To pomeni, da  izračunamo tako, da namesto
izračunamo tako, da namesto  vstavimo neko poljubno število.
vstavimo neko poljubno število.
Vrednosti spremenljivke  so povsem poljubna števila, ki niso odvisna od ničesar, zato spremenljivko
so povsem poljubna števila, ki niso odvisna od ničesar, zato spremenljivko  imenujemo neodvisna spremenljivka.
imenujemo neodvisna spremenljivka.
Vrednosti spremenljivke  so točno določena števila, ki so odvisna od števil
so točno določena števila, ki so odvisna od števil 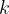 in
in 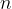 ter od vrednosti
ter od vrednosti  , ki jo vstavimo v enačbo. Zato spremenljivko
, ki jo vstavimo v enačbo. Zato spremenljivko  imenujemo odvisna spremenljivka.
imenujemo odvisna spremenljivka.
Temu odnosu lahko še drugače rečemo, da je  funkcija
funkcija  -a. Zato bomo zgornji zapis pogosto opazili v funkcijski obliki, v katerem
-a. Zato bomo zgornji zapis pogosto opazili v funkcijski obliki, v katerem  zamenjamo z
zamenjamo z 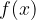 :
:
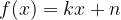
Število 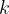 imenujemo smernega koeficient,
imenujemo smernega koeficient, 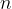 pa začetna vrednost.
pa začetna vrednost.
Če zapišemo vrednosti 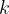 in
in 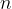 , potem je funkcija natančno določena in lahko narišemo tudi njen graf:
, potem je funkcija natančno določena in lahko narišemo tudi njen graf:
smerni koeficient 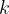 določa strmino premice,
določa strmino premice,
začetna vrednost 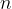 pa presečišče premice z
pa presečišče premice z  osjo.
osjo.
Premico 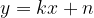 natančno določimo tako, da za
natančno določimo tako, da za 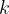 in
in 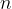 zapišemo številski vrednosti. S tem premico lahko tudi narišemo.
zapišemo številski vrednosti. S tem premico lahko tudi narišemo.
Funkcijo si lahko predstavljamo kot napravo, v katero dajemo števila  , ven pa prihajajo spremenjene vrednosti
, ven pa prihajajo spremenjene vrednosti  . V matematičnem jeziku to pomeni, da v funkcijo vstavljamo poljubna števila
. V matematičnem jeziku to pomeni, da v funkcijo vstavljamo poljubna števila  , izračunamo pa vrednosti funkcije
, izračunamo pa vrednosti funkcije  .
.
Ker  izračunamo po funkcijskem predpisu, vrednost funkcije raje označujemo z
izračunamo po funkcijskem predpisu, vrednost funkcije raje označujemo z 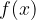 kot z
kot z  . Funkcija ima namreč pri vsakem
. Funkcija ima namreč pri vsakem  drugačno vrednost. Funkcijski zapis je zato bolj primeren, saj z njim zapišemo, pri katerem
drugačno vrednost. Funkcijski zapis je zato bolj primeren, saj z njim zapišemo, pri katerem  nas zanima vrednost funkcije.
nas zanima vrednost funkcije.
Graf linearne funkcije sestavlja neskončna množica točk v obliki premice.
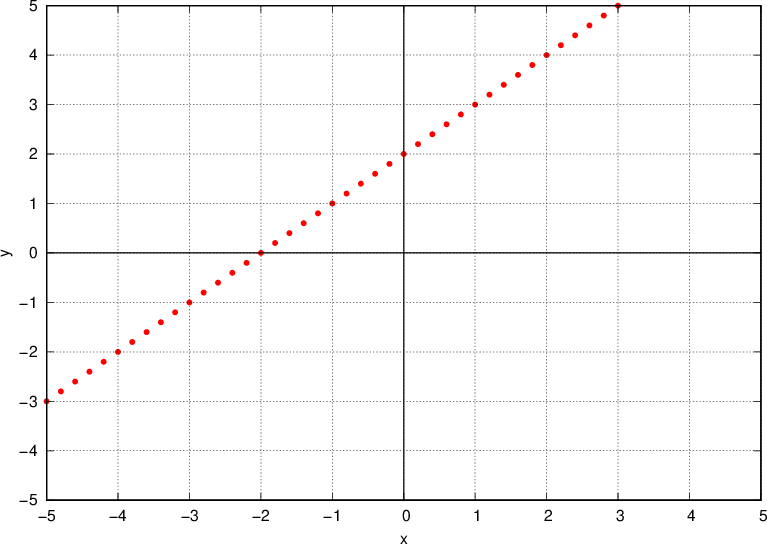
Točka v koordinatnem sistemu 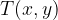 je podana z dvema vrednostma, absciso
je podana z dvema vrednostma, absciso  in ordinato
in ordinato  .
.
Neka točka lahko leži na premici ali pa ne. Velja, da za dani  obstaja samo en
obstaja samo en  , tako da ta točka
, tako da ta točka 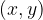 leži na premici.
leži na premici.
Za poljubno točko 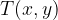 moramo preveriti, če leži na grafu funkcije
moramo preveriti, če leži na grafu funkcije 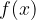 . To naredimo tako, da koordinato
. To naredimo tako, da koordinato  točke vstavimo v predpis funkcije. Če je
točke vstavimo v predpis funkcije. Če je  koordinata točke enaka kot izračunana vrednost funkcije pri danem
koordinata točke enaka kot izračunana vrednost funkcije pri danem  -u, potem vemo, da točka leži na grafu funkcije.
-u, potem vemo, da točka leži na grafu funkcije.
Smerni koeficient nam opiše strmino premice.
Del klanca iz gornjega primera si predstavljamo kot premico v koordinatnem sistemu. Opišemo jo s predpisom:
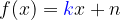
Število 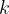 v predpisu premice je smerni koeficient in nam pove, kako strma je premica. Bolj kot je premica strma, bolj je navpična.
v predpisu premice je smerni koeficient in nam pove, kako strma je premica. Bolj kot je premica strma, bolj je navpična.
Ko vidimo premico v koordinatnem sistemu, se po njeni strmini vprašamo na naslednji način. Postavimo se na neko točko premice. Če se  poveča za eno enoto, za koliko se pri tem spremeni
poveča za eno enoto, za koliko se pri tem spremeni  na premici?
na premici?
Če vrednost neodvisne spremenljivke  spremenimo za eno enoto, se vrednost funkcije
spremenimo za eno enoto, se vrednost funkcije  spremeni za
spremeni za 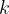 enot.
enot.
V primeru smo videli, da lahko za določitev smernega koeficienta opazujemo dve poljubni točki na premici. Za ti dve točki nas zanima:
koliko se razlikujeta njuni  koordinati in
koordinati in
koliko se razlikujeta njuni  koordinati.
koordinati.
Iz teh dveh razlik oziroma sprememb koordinat določimo smerni koeficient premice kot količnik med spremembo  in spremembo
in spremembo  . Za spremembo
. Za spremembo  koordinate pri dveh točkah premice lahko rečemo tudi, da se je za toliko spremenila vrednost funkcije. Na osi
koordinate pri dveh točkah premice lahko rečemo tudi, da se je za toliko spremenila vrednost funkcije. Na osi  namreč razberemo vrednost funkcije
namreč razberemo vrednost funkcije 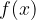 .
.
Smerni koeficient 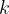 je količnik med spremembo vrednosti funkcije
je količnik med spremembo vrednosti funkcije 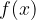 in spremembo vrednosti neodvisne spremenljivke
in spremembo vrednosti neodvisne spremenljivke  :
:
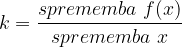
Obravnavamo tri področja vrednosti smernega koeficienta:
Vrednost 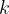 je večja od 0: z večanjem vrednosti neodvisne spremenljivke
je večja od 0: z večanjem vrednosti neodvisne spremenljivke  se veča tudi vrednost funkcije.
se veča tudi vrednost funkcije.
Vrednost 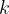 je enaka 0: vrednost funkcije je vedno enaka.
je enaka 0: vrednost funkcije je vedno enaka.
Vrednost 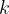 je manjša od 0: z večanjem vrednosti neodvisne spremenljivke
je manjša od 0: z večanjem vrednosti neodvisne spremenljivke  se vrednost funkcije manjša.
se vrednost funkcije manjša.
Smerni koeficient določa strmino premice na naslednji način:
Če je smerni koeficient linearne funkcije pozitiven, je graf naraščajoča premica.
Če je smerni koeficient linearne funkcije enak 0, je graf vodoravna premica.
Če je smerni koeficient linearne funkcije negativen, je graf padajoča premica.
Število 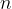 v zapisu linearne funkcije
v zapisu linearne funkcije
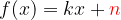
imenujemo začetna vrednost. Pove nam, pri kateri vrednosti  bo premica sekala ordinatno os.
bo premica sekala ordinatno os.
Graf linearne funkcije seka ordinatno os v točki 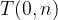 . Velja namreč, da je pri vsaki točki na osi
. Velja namreč, da je pri vsaki točki na osi  , koordinata
, koordinata  enaka 0.
enaka 0.
Začetna vrednost je vrednost funkcije pri vrednosti neodvisne spremenljivke 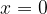 .
.
Ničla linearne funkcije je tisti  , pri katerem graf premice seka abscisno os. Ničlo označimo z
, pri katerem graf premice seka abscisno os. Ničlo označimo z 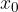 .
.
Zakaj ji rečemo ničla funkcije? Zato ker je v tej točki vrednost funkcije 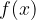 enaka 0. Ali povedano drugače: točka, kjer funkcija seka
enaka 0. Ali povedano drugače: točka, kjer funkcija seka  os, ima koordinato
os, ima koordinato  enako 0.
enako 0.
Graf linearne funkcije torej seka abscisno os v točki 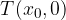 .
.
Ničla linearne funkcije je vrednost neodvisne spremenljivke  pri vrednosti funkcije
pri vrednosti funkcije 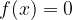 .
.
Graf linearne funkcije lahko narišemo na dva načina:
s tabeliranjem funkcije - izračunamo nekaj točk, ki ležijo na premici
z uporabo začetne vrednosti in smernega koeficienta.
Graf linearne funkcije najlažje narišemo tako da si izberemo nekaj vrednosti neodvisne spremenljivke  in jih zapišemo v tabelo. Običajno si izberemo nekaj
in jih zapišemo v tabelo. Običajno si izberemo nekaj  -ov blizu 0:
-ov blizu 0:
Nato za te vrednosti  izračunamo vrednost
izračunamo vrednost  po predpisu funkcije
po predpisu funkcije 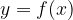 . Tako dobimo urejene pare
. Tako dobimo urejene pare 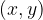 . Pravimo, da funkcijo tabeliramo.
. Pravimo, da funkcijo tabeliramo.
Vsak urejen par predstavlja eno točko na grafu funkcije. Točke narišemo v koordinatni sistem in skozi njih potegnemo premico.
V drugem načinu za risanje grafa linearne funkcije 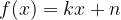 pa uporabimo vrednosti parametrov
pa uporabimo vrednosti parametrov 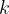 in
in 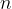 iz predpisa funkcije:
iz predpisa funkcije:
začetna vrednost 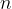 nam da eno točko na premici - presečišče
nam da eno točko na premici - presečišče 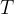 premice z
premice z  osjo.
osjo.
z uporabo smernega koeficienta dobimo še drugo točko na premici, tako da se iz točke 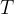 premaknemo za eno enoto v smeri
premaknemo za eno enoto v smeri  v desno in za
v desno in za 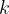 enot v smeri
enot v smeri  .
.
Ko imamo dve točki na premici, lahko skozi njiju potegnemo premico.
Postopek si oglejmo na primeru.
Če nimamo podane začetne vrednosti, lahko uporabimo tudi poljubno drugo točko, za katero vemo, da leži na premici.