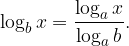Osebne zbirke
Prijava z e-naslovom
Prijava brez gesla
Logaritmiranje je obratna operacija od potenciranja.
Logaritme so najprej uvedli v astronomiji, da bi si poenostavili računanje z velikimi števili, uporablja pa se za določanje pH vrednosti raztopin, lestvico za glasnost zvoka in lestvico za določanje svetlosti zvezd.
Kako pridemo do vpeljave logaritma si poglejmo na naslednjem primeru:
V zgornjem primeru števila y ni bilo težko najti. V splošnem pa tak eksponent (število y) najdemo le s pomočjo logaritma.
Logaritem pozitivnega števila x s pozitivno in od 1 različno osnovno a je tisti eksponent y, pri katerem je potenca z osnovo a enaka številu x:
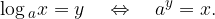
Poglejmo si elemente logaritma:
Poglejmo si še nekaj primerov:
Desetiški logaritem je logaritem z osnovo 10.
Po dogovoru pri desetiškem logaritmu osnove ne pišemo:
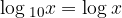
Pri računanju desetiškega logaritma, si lahko pomagamo z žepnim računalom, ki vsebuje ustrezno tipko log.
Naravni logaritem je logaritem z osnovo e.
Za naravni logaritem se je uveljavila naslednja oznaka:
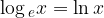
Pri računanju naravnega logaritma, si lahko pomagamo z žepnim računalom, ki vsebuje ustrezno tipko ln.
Logaritmiranje je postopek, s katerim eksponentno enačbo
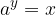
prevedemo v logaritemsko
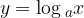
antilogaritmiranje pa nam logaritemsko enačbo prevede v eksponentno enačbo. Logaritmiranje in antilogaritmiranje sta si torej obratni operaciji.
Če logaritemska in eksponentna funkcija nastopata skupaj, ena kot eksponent, druga kot osnova, ali obratno, za vsak a > 0 velja:
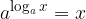
in
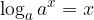
Logaritem produkta števil, ki sta večji od 0 je enak vsoti logaritmov posameznih faktorjev:
Logaritem produkta je vsota logaritmov:
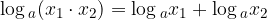
Dokažimo zgornjo enakost. Naj bosta
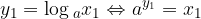
in
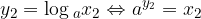
Zapišimo produkt
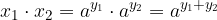
Če logaritmiramo zgornji izraz dobimo:
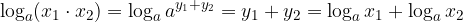
Logaritem kvocienta števil, ki sta večji od 0 je enak razliki logaritmov deljenca in delitelja.
Logaritem kvocienta je enak razliki logaritmov:
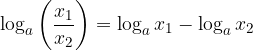
Dokaz je podoben prejšnjemu.
Logaritem potence je enak produktu eksponenta in logaritma osnove.
Logaritem potence:
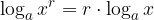
Dokažimo. Naj bo
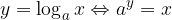
Potem sledi:
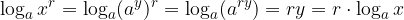
Ko računamo primere v katerih nastopajo logaritmi želimo velikokrat uporabiti računalo, ki pa nam izračuna le desetiški in naravni logaritem. Zato logaritem pretvorimo na ustrezno osnovo:
Pri prehodu iz osnove b k novi osnovi a uporabljamo obrazec:
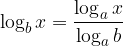
Izpeljimo obrazec. Logaritem z osnovo b označimo z
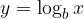
ki ga po definiciji zapišemo kot
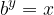
Zgornjo enakost logaritmiramo z logaritmom, ki ima osnovo a in uporabimo logaritem potence.
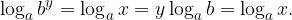
Sedaj y nadomestimo z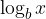 
in dobimo zvezo:
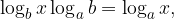
ki je po preoblikovanju enaka našemu obrazcu:
