

Ko smo spoznavali naravna števila, smo rekli, da so to števila, s katerimi štejemo: 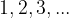
Za opisovanje sveta okoli sebe pa naravna števila niso dovolj.
Če želimo meriti in opisovati količine, katerih vrednost je lahko enaka 0 ali manj, moramo množici naravnih števil dodati še število 0 in negativna števila.
Na ta način nastane nova, razširjena množica, ki jo imenujemo množica celih števil.
Množico celih števil sestavljajo naslednje podmnožice:
množica pozitivnih celih števil oziroma množica naravnih števil:
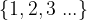
množica z elementom 0:
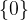
množica negativnih celih števil:
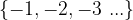
Množico celih števil označimo s črko 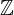 , podmnožico pozitivnih celih števil z
, podmnožico pozitivnih celih števil z 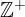 , podmnožico negativnih celih števil z
, podmnožico negativnih celih števil z 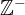 , podmnožico z elementom 0 pa kot
, podmnožico z elementom 0 pa kot 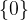 .
.
Oznako za naravna števila 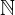 pa že poznamo od prej.
pa že poznamo od prej.
Množica celih števil je sestavljena iz treh množic: množice negativnih celih števil, množice s številom 0 in množice pozitivnih celih števil. To z matematičnimi znaki zapišemo na naslednji način:
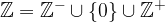
Množica pozitivnih celih števil je enaka množici naravnih števil:
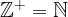
Kadar neko število pripada več množicam hkrati, potem za njegov opis vedno vzamemo najbolj strogo oziroma najmanjšo množico.
Številsko premico, ki jo poznamo že iz obravnave naravnih števil, podaljšamo levo od števila 0:
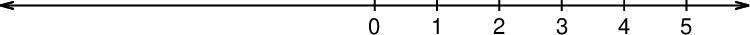
Enako enoto (razdaljo med posameznimi števili) nanesemo še levo od števila 0. Točke na levi strani premice poimenujemo enako kot točke na desni, le da jim spredaj zapišemo predznak "-". Številu 0 sledi število -1, nato -2 in tako naprej.
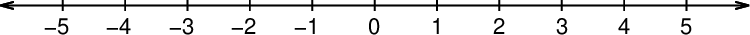
Števila levo od 0 imenujemo negativna števila, števila desno od 0 pa pozitivna števila.
Pozitivna števila so večja od 0, negativna števila pa so manjša od 0.
Negativna števila imajo pred seboj negativni predznak "-".
Razvrstitev števil po velikosti si najlažje ogledamo na številski premici. Velja preprosto pravilo: števila naraščajo od leve proti desni. Tako je poljubno število večje od vseh, ki od njega ležijo levo.
Tako kot velja za naravna števila, velja tudi za cela števila:
Najmanjše izmed danih števil je na številski premici prikazano najbolj levo, največje število pa najbolj desno.
Zgornjo trditev lahko zapišemo tudi drugače:
Večje število na številski premici vedno leži desno od manjšega.
Če se po številski premici premikamo v levo stran, se vrednost manjša (negativna sprememba), če se premikamo desno, pa se veča (pozitivna sprememba).
Najlažje po velikosti razvrstimo eno pozitivno in eno negativno število:
Katero koli pozitivno število je vedno večje od katerega koli negativnega števila.
Če poljubno celo število preslikamo čez izhodišče 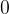 številske premice, dobimo njegovo nasprotno vrednost.
številske premice, dobimo njegovo nasprotno vrednost.
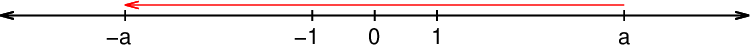
Število in njegovo nasprotno število sta enako oddaljena od števila 0.
Nasprotna vrednost pozitivnega števila je negativno število, nasprotna vrednost negativnega števila pa je pozitivno število.
Nasprotni si števili imata enako številsko vrednost in različen predznak.
Kaj pa dobimo, če številu prištejemo njegovo nasprotno vrednost? Če poljubnemu številu prištejemo njegovo nasprotno vrednost, je rezultat enak 0.
Vsota nasprotnih števil je enaka 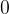 :
:
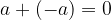
Preden pričnemo računati s celimi števili, razjasnimo pomene matematičnih simbolov:
"+"
"-"
Oba simbola imata več pomenov.
Simbol "plus" lahko pomeni:
pozitivni predznak celega števila ali pa
računsko operacijo seštevanja.
Predznak vedno zapišemo tik ob številu na levi strani in pripada številu. Pozitivnega predznaka običajno ne pišemo, razen če ga želimo izrecno poudariti.
Plus kot računsko operacijo seštevanja pa zapišemo med dve števili, ki ju želimo sešteti.
Simbol "minus" lahko pomeni:
negativni predznak celega števila,
računsko operacijo odštevanja ali pa
oznako za nasprotno število.
Predznak minus vedno zapišemo tik ob številu na levi strani in pripada številu. Negativni predznak moramo vedno zapisati.
Minus kot računsko operacijo odštevanja zapišemo med dve števili, ki ju želimo odšteti.
Med računsko operacijo in predznakom vedno pišemo oklepaj.
Če število 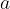 preslikamo čez izhodišče, dobimo njegovo nasprotno vrednost
preslikamo čez izhodišče, dobimo njegovo nasprotno vrednost 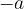 . Če nato število
. Če nato število 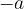 še enkrat preslikamo čez izhodišče, dobimo spet prvotni
še enkrat preslikamo čez izhodišče, dobimo spet prvotni 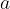 .
.
Nasprotna vrednost nasprotne vrednosti števila je število samo:
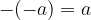
Absolutna vrednost števila pomeni razdaljo na številski premici:
od izhodišča (točka 0)
do točke, ki označuje število.
Absolutno vrednost poljubnega števila 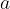 označimo tako, da število postavimo med dve pokončni črti:
označimo tako, da število postavimo med dve pokončni črti:
Razdalo v pozitivno smer in v negativno smer številske premice obravnavamo enako:
Razdalja ne more biti negativna, zato je absolutna vrednost pozitivno število. Izjema je le število 0, katerega absolutna vrednost je enaka 0. Število 0 pa ni niti negativno niti pozitivno, ampak mu rečemo nenegativno število.
Absolutna vrednost poljubnega celega števila, različnega od 0, je vedno pozitivno število.
Oglejmo si še primer povezave med nasprotno in absolutno vrednostjo števila:
Absolutni vrednosti nasprotnih števil sta enaki.
Pri razlagi računskih operacij s celimi števili si bomo pomagali s številsko premico, na kateri števila naraščajo od leve proti desni.
Če neko število povečamo, se premakne v desno stran, če pa ga zmanjšamo, se premakne v levo stran.
Računske operacije v okviru celih števil so podobne tistim, ki jih že poznamo iz naravnih števil, le da jih še nekoliko razširimo. Najpomembnejša dopolnitev se nanaša na negativne predznake in nasprotno vrednost.
Najprej si poglejmo računsko operacijo seštevanja.
Pozitivnemu številu a prištejmo pozitivno število b. To je enostaven primer, ki ga poznamo že od naravnih števil.
Pozitivno število a je na številski osi prikazano desno od števila 0:
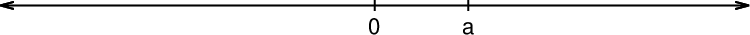
Če temu številu prištejemo pozitivno vrednost, se mu vrednost poveča, zato se premakne v desno. Tudi vsota se nahaja desno od števila 0:
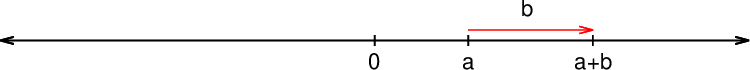
Vsota števil je od izhodišča številske osi oddaljena toliko kot seštevek posameznih števil.
Zanima nas, kakšna je lahko razlika dveh celih števil:
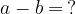
Pri naravnih številih smo lahko odštevali le takšni števili, da je bil rezultat pozitiven. Odštevanec b je moral biti torej manjši od zmanjševanca a.
V množici celih števil pa je b lahko tudi večji od a.
Pozitivno število a je na številski osi prikazano desno od števila 0:
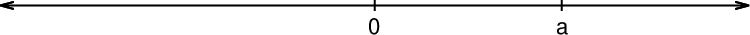
Če temu številu odštejemo pozitivno število b, se mu vrednost zmanjša. Od števila a se geometrijsko zato premikamo v levo. Razlika števil je lahko:
pozitivna,
enaka 0,
negativna.
Razlika je odvisna od velikosti števila b.
V primeru, da je število b manjše od števila a, je razlika 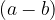 pozitivna in se nahaja desno od števila 0:
pozitivna in se nahaja desno od števila 0:
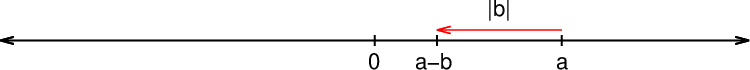
V primeru, da je število b enako številu a, se razlika nahaja v izhodišču številske osi:

V primeru, da je število b večje od števila a, se razlika nahaja levo od števila 0 in je zato negativna:

Negativna števila razumemo kot nasprotna števila od pozitivnih števil. Zato si poglejmo seštevanje in odštevanje nasprotne vrednosti števil.
Vrnimo se na trditev, da je vsota enako velikih nasprotnih vrednosti enaka 0:
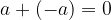
Če številu prištejemo njegovo nasprotno vrednost, je rezultat torej enak 0, kot če bi število odšteli od samega sebe:
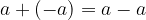
Gornja enakost je pravilo, ki velja tudi splošneje za dve poljubni števili 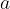 in
in 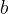 . Če nekemu številu prištejemo nasprotno vrednost poljubnega števila, je rezultat enak, kot če bi to število odšteli.
. Če nekemu številu prištejemo nasprotno vrednost poljubnega števila, je rezultat enak, kot če bi to število odšteli.
Prištevanje nasprotne vrednosti števila je enako odštevanju števila:
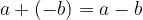
Če enakost preberemo iz nasprotne smeri pa vidimo, da lahko odštevanje zapišemo v obliki prištevanja nasprotnega števila:
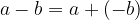
Kaj pa odštevanje nasprotne vrednosti? Če od števila odštejemo njegovo nasprotno vrednost, je to enako prištevanju števila.
Odštevanje nasprotne vrednosti števila je enako prištevanju števila:
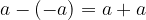
Gornje pravilo lahko preverimo z reševanjem enačb z operacijami nad enačbami. Izhajali bomo iz prejšnjega pravila za prištevanje nasprotne vrednosti in ga preoblikovali:
Pravilo velja tudi splošno za poljubni števili 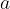 in
in 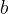 :
:
Odštevanje nasprotne vrednosti števila je enako prištevanju števila:
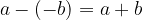
Opisana pravila za prištevanje in odštevanje nasprotne vrednosti nam bodo v nadaljevanju služila za osnovo pri računanju z negativnimi celimi števili.
Če števila v matematičnem izrazu vsebujejo predznake, so ta zapisana v oklepaju, da predznake ločimo od simbolov za računske operacije.
Za lažje računanje je priporočljivo znak za računsko operacijo in predznak združiti v en simbol, s čimer oklepaj ni več potreben.
Z uporabo gornjih dveh pravil za prištevanje in odštevanje nasprotne vrednosti sestavimo preglednejšo tabelo vseh kombinacij prištevanja in odštevanja pozitivnega ali negativnega števila:
Ogledali smo si že skoraj vse kombinacije seštevanja in odštevanja celih števil. Preostali so nam le še primeri, ko prištevamo ali odštevamo od negativnega števila.
Prvi znak "-" stoji levo od števila 3, torej gre za predznak. Drugi znak "-" pa stoji med dvema številoma, kar pomeni, da predstavlja računsko operacijo odštevanja. Imamo torej primer odštevanja od negativnega števila.
V poglavju o odštevanju pozitivnih števil smo spoznali, da je:
pri odštevanju rezultat manjši od vrednosti prvega člena v računu, kar geometrijsko pomeni premik v levo,
pri prištevanju rezultat večji od vrednosti prvega člena v računu, kar geometrijsko pomeni premik v desno.
Enako velja tudi v primeru, ko je prvi člen v računu negativno število.
Število, ki ga negativnemu številu prištevamo ali odštevamo, je lahko tudi negativno. V tem primeru se računanja lotimo tako, da:
najprej poenostavimo zapis za računsko operacijo in predznak, tako da znaka združimo v en simbol in se znebimo oklepajev, nato pa
računamo na enak način kot pri prištevanju in odštevanju pozitivnega števila.
Spodnji primer povzema vse do sedaj naučeno v nekoliko drugačni obliki, ki je primerna predvsem za učence s prevladujočim vizualnim načinom učenja:
Račune seštevanja in odštevanja več števil z različnimi predznaki običajno izračunamo tako, da zapis po potrebi najprej poenostavimo, nato pa ga po vrsti izračunamo od leve proti desni.
Celi števili zmnožimo tako, da množimo njuni absolutni vrednosti, predznak pa določimo po naslednjem pravilu:
če množimo dve pozitivni števili, dobimo pozitiven rezultat,
če množimo eno pozitivno in eno negativno število, dobimo negativen rezultat,
če množimo dve negativni števili, dobimo pozitiven rezultat.
Pravila predstavimo še s tabelo:
Če množimo več celih števil, predznak produkta določimo po naslednjem pravilu:
Če je število negativnih faktorjev sodo, potem je rezultat pozitiven.
Če je število negativnih faktorjev liho, je rezultat negativen.
Zmnožek celega števila s številom 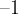 je enak nasprotni vrednosti števila:
je enak nasprotni vrednosti števila:
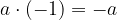
Kadar množimo:
število in spremenljivko ali
dve spremenljivki
lahko znak za množenje opustimo. V teh primerih privzamemo, da je med elementi operacija množenje in ne kaj drugega.
Kadar množimo dve števili, moramo znak za množenje nujno zapisati.
Izpustimo lahko tudi znak za množenje ob oklepaju in med oklepaji.
Celi števili delimo tako, da delimo njuni absolutni vrednosti, predznak pa določimo po naslednjem pravilu:
če delimo dve pozitivni števili, dobimo pozitiven rezultat,
če delimo eno pozitivno in eno negativno število, dobimo negativen rezultat,
če delimo dve negativni števili, dobimo pozitiven rezultat.
Pravila predstavimo še s tabelo: