Osebne zbirke


Svet, ki nas obkroža, je obdan iz elementov in spojin, ki tvorijo različne snovi. Atomi elementov so majhni in nezaznavni za človeško oko. Zaradi svoje majhnosti jih ne moremo tehtati. Njihovo velikost oziroma težo lahko samo primerjalno določimo.
Težo elementov določamo s pomočjo standarda. Standard, ki so ga postavili v ta namen, je masa ogljikovega atoma 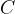 . Maso drugih atomov in spojin pogosto izražamo kot večkratnik mase ogljikovega atoma
. Maso drugih atomov in spojin pogosto izražamo kot večkratnik mase ogljikovega atoma 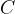 . Maso, ki jo izrazimo na tak način, imenujemo:
. Maso, ki jo izrazimo na tak način, imenujemo:
relativna atomska masa, če izražamo maso atomov oziroma
relativna molekulska masa, če izražamo maso molekul.
Relativna molekulska masa je število, ki pove, kolikokrat je masa molekule večja od ene dvanajstine mase atoma ogljikovega izotopa 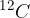 . Označimo jo z
. Označimo jo z 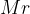 in nima enot.
in nima enot.
Relativno molekulsko maso dobimo iz periodnega sistema elementov s seštevanje relativnih atomskih mas posameznih atomov, ki so prisotni v molekuli:
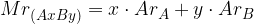
Poglejmo si izračun relativne molekulske mase na konkretnem primeru.
Pri kemijskem računanju namesto relativnih molekulskih mas pogosto uporabljamo molsko maso. Molska masa je masa enega mola snovi. Označujemo jo z 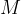 in ima enoto
in ima enoto 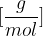 .
.
Molska masa je masa molekul v enem molu snovi.
Molska masa je številčno enaka relativni molekulski masi. Razen tega, da je njun pomen drugačen, je molska masa opremljena z enoto.
Pri opisu molske mase snovi smo omenili besedo mol. Mol je osnovna enota, s katero merimo množino. Množina je tista količina, ki nam pove število delcev v dani snovi.
Množino označujemo s simbolom 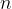 in kot smo že omenili ima enoto
in kot smo že omenili ima enoto 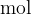 . Ko rečemo, da imamo 1 mol snovi, s tem mislimo, da imamo
. Ko rečemo, da imamo 1 mol snovi, s tem mislimo, da imamo 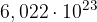 delcev te snovi. Pri tem ni pomembno, za katero snov gre.
delcev te snovi. Pri tem ni pomembno, za katero snov gre.
Pri tem tudi ni pomembno, za kateri delec gre. Ko govorimo v molih lahko govorimo o atomih, molekulah in raznovrstnih delcih.
Mol se tako ne nanaša samo na molekule, ampak na delce, ki so prisotni v katerikoli snovi.
Število molekul (delcev, atomov), izbrane snovi je definirano na podlagi ogljikovega atoma, kot referenčnega atoma. Zato je dobro poznana tudi naslednja definicija mola:
En mol je tista količina snovi, ki ima enako število delcev (atomov ali molekul), kot je atomov v 12 gramih izotopa ogljika 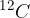 .
.
V 12g ogljikovega izotopa 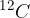 se nahaja
se nahaja 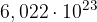 atomov. To število imenujemo Avogadrova konstanta.
atomov. To število imenujemo Avogadrova konstanta.
Avogadrovo število (konstanta) je tista količina, ki povezuje število delcev z množino snovi. Označujemo jo s simbolnim zapisom 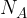 in znaša
in znaša
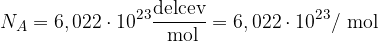
Različne količine, ki opisujejo množino snovi, lahko povežemo med seboj, saj je množina je definirana kot kvocient med številom delcev in avogadrovim številom:
Množina snovi n je povezana s številom delcev snovi:
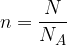
kjer je
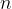 množina snovi z enoto
množina snovi z enoto 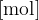
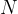 število delcev in nima enot
število delcev in nima enot
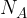 Avogadrovo število z enoto
Avogadrovo število z enoto 
Podobno lahko povežemo tudi maso snovi z množino. Množino lahko izračunamo tudi kot kvocient med maso snovi in njeno molsko maso.
Masa snovi je povezana z množino snovi s formulo:
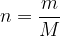
kjer je:
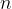 množina snovi z enoto
množina snovi z enoto 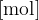
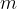 masa snovi z enoto [g]
masa snovi z enoto [g]
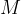 molska masa z enoto
molska masa z enoto