Osebne zbirke


Neskončna geometrijska vrsta je poseben primer neskončne vrste, zato najprej spoznajmo neskončno vrsto.
Neskončna vrsta je vsota neskončno mnogo členov nekega zaporedja števil 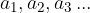 :
:
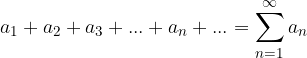
Splošni člen neskončne vrste označimo z:
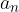
Neskončno vrsto (ki ji sicer rečemo tudi vsota) pa z veliko grško črko sigma:
Zapišimo vsote prvih n členov zaporedja:
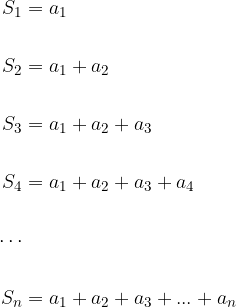
Dobljene vsote imenujemo delne vsote zaporedja. Označujemo jih z 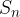 . Zaporedje
. Zaporedje 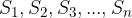 pa imenujemo zaporedje delnih vsot.
pa imenujemo zaporedje delnih vsot.
Vsota neskončne vrste 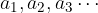 je limita zaporedja delnih vsot, ko gre
je limita zaporedja delnih vsot, ko gre 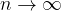 . Limito zaporedja delnih vsot označimo z S in zapišemo:
. Limito zaporedja delnih vsot označimo z S in zapišemo:
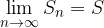
Vsota neskončne vrste je:
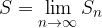
Kadar limita zaporedja delnih vsot obstaja, rečemo, da vrsta 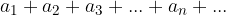 konvergira k vsoti S oz. je konvergentna z vsoto S. To pomeni, da lahko seštejemo neskončno število členov zaporedja.
konvergira k vsoti S oz. je konvergentna z vsoto S. To pomeni, da lahko seštejemo neskončno število členov zaporedja.
Kadar pa limita delnih vsot ne obstaja oziroma je njena vrednost neskončna, rečemo, da vrsta divergira oz. je divergentna. To pomeni, da ne moremo sešteti neskončno število členov zaporedja.
Predstavljajmo si, da imamo dano neskončno geometrijsko zaporedje 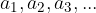 in želimo izračunati njegovo vsoto
in želimo izračunati njegovo vsoto 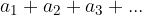 . Za izračun vsote danega zaporedja uporabimo neskončno geometrijsko vrsto. Ker gre za geometrijsko zaporedje, vemo, da velja:
. Za izračun vsote danega zaporedja uporabimo neskončno geometrijsko vrsto. Ker gre za geometrijsko zaporedje, vemo, da velja: 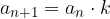 , zato lahko vrsto namesto:
, zato lahko vrsto namesto:
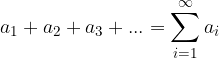
zapišemo kot:
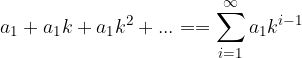
Vemo, da je vrsta konvergentna, če obstaja limita delnih vsot, zato poiščimo vsoto za prvih n členov:
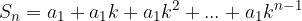
Zapis prepoznamo kot končno geometrijsko vrsto, zato ga lahko krajše zapišemo z uporabo obrazca za izračun vsote končne geometrijske vrste:
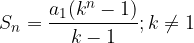
Če je naša vrsta konvergentna, potem obstaja limita njenih delnih vsot S:
Opazimo, da bo limita delnih vsot obstajala, če bo obstajala limita potenčnega zaporedja 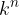 . Pa razmislimo, kdaj obstaja limita potenčnega zaporedja:
. Pa razmislimo, kdaj obstaja limita potenčnega zaporedja:
vrednosti potence 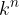 se z naraščanjem eksponenta n stekajo proti nič, če za osnovo potence k velja
se z naraščanjem eksponenta n stekajo proti nič, če za osnovo potence k velja 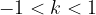 . Zato velja:
. Zato velja:
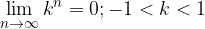
Za ostale osnove potence k limita očitno ne obstaja.
Zaključimo, da limita delnih vsot obstaja, če velja:
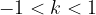
oz.

Izračunamo limito delnih vsot (1) do konca:
Vsota neskončne geometrijske vrste je tako: