Osebne zbirke
Prijava z e-naslovom
Prijava brez gesla
Neskončna limita je limita, ki naraste čez vse vrednosti, ko se naša variabila bliža limitni vrednosti. Zapišemo jo kot:
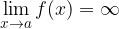
Okolica točke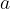 
je odprt interval okoli 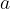s središčem v 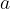. Odprti interval 
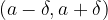imenujemo 
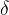(delta) okolica števila 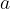. Širina tega intervala je odvisna od pozitivnega števila 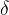, ki je ponavadi zelo majhen.
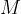je realna vrednost, ki leži na 
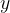-osi. Pri neskončni limiti predstavlja mejo, čez katero rastejo funkcijske vrednosti 
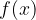, ko se 
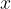približuje vrednosti .
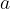Limita je neskončna, če za poljubno vrednost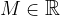 
, da lahko najdemo tak 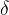, da ko bo x v 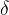-okolici točke a, torej 
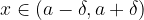, bo 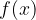večja od .
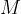Limita
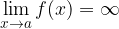
je neskončna, če za vsak 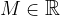obstaja tak 
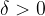, da velja: če je
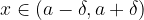
potem sledi
Primer neskončne limite
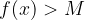
S pomočjo limit lahko določimo potek navpične asimptote v grafu. Če velja, da
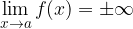
potem ima graf funkcije 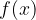navpično asimptoto v 
.
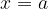Imejmo funkcijo 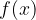. Če velja:
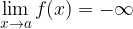
potem povsem enakovredno velja tudi:
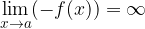
Ponazorimo še grafično (grafa sta simetrična glede na abcisno os):
Funkcija ima negativno neskončno limito
Funkcija 
pa ima pozitivno neskončno limito
