Osebne zbirke


Nihalo na vijačno vzmet je sestavljeno iz vzmeti in uteži z maso 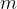 , pritrjeno na vzmet. V začetku utež miruje v ravnovesni legi. Ko maso premaknemo iz ravnovesne lege in nato spustimo, utež zaniha okoli ravnovesne lege.
, pritrjeno na vzmet. V začetku utež miruje v ravnovesni legi. Ko maso premaknemo iz ravnovesne lege in nato spustimo, utež zaniha okoli ravnovesne lege.
Najprej si zamislimo, da drsi utež brez trenja po vodoravni podlagi. Na ta način dosežemo, da je sila teže pravokotna na smer gibanja nihala in ne vpliva na nihanje.
V drugem primeri pritrdimo vzmet z utežjo navpično. Sila teže deluje sedaj v smeri gibanja nihala . Ugotoviti moramo, ali se bo zato frekvenca nihanja kaj spremenila.
Zamislimo si maso 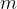 , pripeto na vodoravno vzmet, ki brez trenja drsi po vodoravni podlagi. V ravnovesni legi je sila vzmeti enaka nič. Maso izmaknemo iz ravnovesne lege in jo premaknemo do temenskega odmika. Pri premiku opravljamo delo: napenjamo vzmet in damo nihalu prožnostno energijo. Sedaj utež spustimo. Vsa prožnostna energija se v ravnovesni legi pretvori v kinetično energijo. Od tu naprej se vzmet stiska in energija se ponovno pretvori v prožnostno energijo. Proces se ponavlja.
, pripeto na vodoravno vzmet, ki brez trenja drsi po vodoravni podlagi. V ravnovesni legi je sila vzmeti enaka nič. Maso izmaknemo iz ravnovesne lege in jo premaknemo do temenskega odmika. Pri premiku opravljamo delo: napenjamo vzmet in damo nihalu prožnostno energijo. Sedaj utež spustimo. Vsa prožnostna energija se v ravnovesni legi pretvori v kinetično energijo. Od tu naprej se vzmet stiska in energija se ponovno pretvori v prožnostno energijo. Proces se ponavlja.
Ko nihalo izmaknemo iz ravnovesne lege (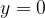 ) za temenski odmik, napnemo vzmet. Sila vzmeti deluje v nasprotno smer, kot je bilo naše gibanje. Deluje zaviralno in je zato negativna. Izračunamo jo po Hookovem zakonu:
) za temenski odmik, napnemo vzmet. Sila vzmeti deluje v nasprotno smer, kot je bilo naše gibanje. Deluje zaviralno in je zato negativna. Izračunamo jo po Hookovem zakonu:

Ko maso spustimo, povzroči sila po II Newtonovem zakonu pospešek:
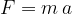
Uporabimo izraz za pospešek pri harmoničnem nihanju:
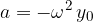
Oba izraza vstavimo v enačbo (1) in dobimo:
Nihalo pritrdimo navpično, kot kaže slika. Ali bo navpična lega nihala zaradi teže telesa kaj vplivala na frekvenco nihanja?
Oglejmo si sliko. Neraztegnjeni vzmeti (A) dodamo utež (B). Zaradi sile teže se vzmet raztegne za 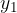 . To je nova ravnovesna lega. Sila teže
. To je nova ravnovesna lega. Sila teže 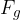 mase
mase 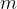 in sila vzmeti
in sila vzmeti 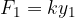 sta si v tej točki v ravnovesju.
sta si v tej točki v ravnovesju.

Z dodatno silo roke 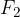 potegnemo vzmet navzdol za
potegnemo vzmet navzdol za 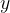 . Sedaj je sila vzmeti:
. Sedaj je sila vzmeti:
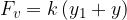
Navzdol delujeta še sila teže in dodatna sila 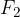 . Dokler ne odmaknemo roke, je njihova rezultanta enaka nič:
. Dokler ne odmaknemo roke, je njihova rezultanta enaka nič:
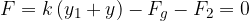
Sedaj spustimo utež (C). Ker je sedaj sila roke enaka 0, dobimo rezultančno silo:
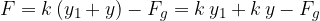
Z upoštevanjem enačbe (2) dobimo:
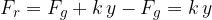
Rezultat je enak, kot če bi utež ležala vodoravno, zato se frekvenca ne bo spremenila. Nihalo bo nihalo kot v prvem primeru.
Vijačna vzmet ima krožno frekvenco:
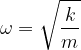
frekvenca:
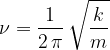
in nihajni čas: