Prijava z e-naslovom
Prijava brez gesla
Odstotek je zapis za del celote. Tako kot ulomek.
Že ime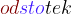 
nam pove, da z odstotki povemo, koliko od sto delov celote imamo. En odstotek je torej majhen del celote oziroma ena stotina celote.
Kot vidimo, so odstotki in ulomki zelo povezani - oboje je številka, s katero povemo, kako velik del celote imamo v mislih.
Pri odstotkih celoto vedno razrežemo na 100 delov. Zmanjšan del celote bomo tako v odstotkih predstavili s številko od 0 do 100 in znakom %. Tako si hitro predstavljamo, kako velik del celote imamo. Še enostavneje kot pri ulomkih.
Na primeru si oglejmo nekaj pogostih odstotkov. Običajno jih prikažemo kot del kroga, pravokotnika ali drugega enostavnega lika.
Preden nadaljujemo z uporabo odstotkov, se naučimo, kako odstotke zapišemo v obliki ulomka in decimalne številke. Tako bomo videli, da odstotek ni nič drugega kot navadna številka.
Najprej poglejmo, kako odstotek zapišemo v obliki ulomka. Povedali smo, da en odstotek predstavlja eno stotino celote, kar z ulomkom zapišemo kot:
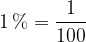
Več odstotkov pomeni več stotin. Oziroma, kolikor odstotkov, toliko stotin imamo.
Vedno, ko imamo podan nek celoštevilski odstotek, ga lahko zapišemo v obliki ulomka z imenovalcem 100. Takšnim ulomkom pravimo desetiški ulomki.
Zatem, ko odstotek pretvorimo v ulomek z imenovalcem 100, tak ulomek še okrajšamo, če lahko.
Odstotek pretvorimo v obliko desetiškega ulomka tako, da:
v števec zapišemo številsko vrednost odstotka,
v imenovalec pa število 100.
Ali obstaja tudi odstotek, ki ga ne moremo zapisati v obliki desetiškega ulomka?
Ja, če je odstotek podan v obliki periodičnega decimalnega števila. Na primer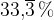 
. Tak odstotek lahko zapišemo v obliki ulomka 
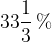. Imamo torej ulomek, le da ta ulomek ni desetiški.
Velja tudi obratno: vsak desetiški ulomek lahko zapišemo kot odstotek, le da tu upoštevamo povezavo med odstotki in ulomki v obratni smeri. Ena stotina celote je en odstotek:
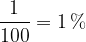
Pred pretvorbo desetiški ulomek preoblikujemo tako, da ima v imenovalcu število 100 in s tem dobimo odstotke.
Desetiški ulomek pretvorimo v odstotek tako, da:
ulomek preoblikujemo na imenovalec 100, nato pa
zapišemo samo števec ulomka, ki mu sledi znak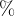 
za odstotek.
Odstotek lahko zapišemo tudi v obliki decimalnega števila.
Tudi tu pri pretvorbi upoštevamo, da vsak odstotek predstavlja eno stotino celote. In zatem število stotin zapišemo kot decimalno število:
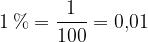
Ker ulomkova črta pomeni deljenje, število odstotkov preprosto delimo s 100 in dobimo decimalno število.
Odstotek pretvorimo decimalno število tako, da številko delimo s 100 in spustimo znak za odstotek.
Tudi decimalno število lahko zapišemo kot odstotek.
V zgornjem primeru smo videli, da je decimalno število 100-krat manjše od odstotne vrednosti.
In zato velja, da je odstotna vrednost 100-krat večja kot decimalno število. Imamo torej več odstotkov kot je velika decimalna številka.
Decimalno število pretvorimo v odstotek tako, da ga množimo s 100 in pripišemo znak za odstotek.
Omenjene pojme celota, del celote in delež celote si najlažje predstavljamo na nekem konkretnem predmetu, na primer torti.
Celoto predstavlja celotna torta, preden jo začnemo rezati na kose,
del celote predstavlja poljubno velik kos torte,
delež celote pa opisuje odstotke, ki jih predstavlja kos torte.
Kot bomo videli v naslednjem primeru, ene količine navajamo v merskih enotah, druge pa v odstotkih.
Celoto in njen del vedno navajamo v merskih enotah ali zgolj s številom elementov, delež pa v odstotkih.
Te tri količine:
celota
del celote
delež celote
so povezane.
Za celoto, del celote in delež velja:
Če poznamo poljubni dve količini, potem lahko izračunamo tretjo.
Poglejmo torej, kako izračunamo vsako od njih.
V nekaterih primerih poznamo celoto in nek del celote. Ne vemo pa, koliko odstotkov ta del celote predstavlja.
Delež izračunamo tako, da del celote delimo s celoto, rezultat pa navedemo v odstotkih:
Delež izračunamo po obrazcu:
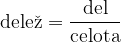
Rezultat v odstotkih navedemo tako, da ga množimo s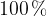 
, tako kot je prikazano v spodnjem primeru. Množenje s 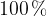pomeni isto kot množenje z 1, le da je to zapisano z odstotki.
Delež celote lahko izračunamo tudi s sklepanjem:
V nekaterih primerih poznamo celoto in velikost dela celote v odstotkih. Ne vemo pa, koliko dejanskih enot (kilogramov, ljudi, ...) predstavlja ta del celote.
Velikost dela celote izračunamo tako, da delež pomnožimo s celoto. Tako nam delež (ki je manjši od 1) zmanjša celoto na del celote.
Del celote izračunamo po obrazcu:
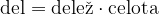
pri čemer je delež podan v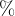 
.
Del celote lahko izračunamo tudi s sklepanjem:
Tudi s sklepanjem smo ugotovili enako: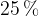 
od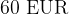 
je torej 
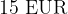oziroma znesek na posamezni položnici je .
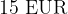Problem, v katerem nastopajo celota, opazovani del celote in delež, lahko rešujemo tudi tako, da besedilo vaje preoblikujemo v matematično enačbo in jo rešimo.
To znanje bomo potrebovali tudi v nadaljevanju, ko bomo računali velikost količine, zatem ko se ta spremeni za nekaj odstotkov.
Pred oblikovanjem enačbe moramo iz naloge razbrati:
celoto,
opazovani del celote in
delež, ki ga predstavlja opazovani del celote
Nato zapišemo stavek v obliki:
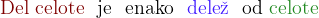
Neznano količino nadomestimo z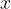 
, znani količini pa s podanimi vrednostmi.
Nazadnje besedo "od" zamenjamo z matematičnim "krat", "je enako" pa z matematičnim enačajem:
Rezultat zamenjave je matematična enačba, ki jo znamo rešiti.
Pri preoblikovanju problema v matematično enačbo moramo besede preoblikovati v matematični zapis:
neznano količino nadomestimo z neznanko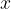 
"je" nadomestimo z enačajem 
"odstotkov" nadomestimo z matematičnim znakom za odstotek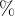 
"od" nadomestimo z množenjem 
Oglejmo si še primer, kjer je neznana količina delež.
V nekaterih primerih poznamo del celote, izražen tako v odstotkih kot v dejanskih enotah (kilogramih, metrih ali številu ljudi), ne vemo pa, koliko enot predstavlja celota.
Celoto izračunamo tako, del delimo z odstotnim deležem. S tem nam delež (ki je manjši od 1) poveča del na celoto.
Celoto izračunamo po obrazcu:
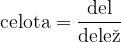
pri čemer je delež podan v .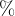
Preverimo ta obrazec z enostavnim primerom.
Tudi celoto lahko izračunamo s sklepanjem:
Poglejmo še količine, ki se spreminjajo.
Na začetku imamo celoto, ki se nato poveča ali zmanjša:
Tej začetni velikosti rečemo tudi osnova in
ta nam vedno predstavlja 100 % količine.
Nato pa velikost naraste ali pade.
Osnova predstavlja 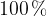količine.
Če se količina poveča, se odstotek poveča nad 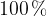. Če pa se količina zmanjša, se odstotek zmanjša pod .
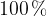V nadaljevanju si bomo ogledali, kako te spremembe računamo z odstotki.
Povečanje količine je pogosto predstavljeno kot podražitev izdelkov in storitev.
Pri povečanju količine nas prav tako zanima del celote. Ta del pa si lahko poljubno izberemo. Lahko opazujemo:
povečanje količine (običajno med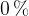 
in 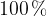količine) ali
novo vrednost količine (nad 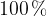količine).
Nova vrednost celote je večja od stare vrednosti celote.
S pomočjo gornjega obrazca rešimo še en primer:
Tudi tu si lahko pomagamo s sklepanjem:
V vsakdanjem življenju zmanjšanje količine pogosto predstavljamo s pocenitvami izdelkov in storitev.
Tudi pri zmanjšanju količine izračunamo del celote tako, da delež množimo s celoto:
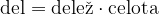
Pri tem nas lahko zanima:
zmanjšanje celote (običajno med 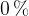in 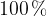količine) ali
nova vrednost celote (odstotni delež, manj od 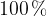količine).
Oglejmo si primer za izračun zmanjšanja celote.
Tudi tu si lahko pomagamo s sklepanjem:
