Osebne zbirke


Če celoto razrežemo na enako velike kose, potem lahko z ulomkom predstavimo želeni del celote.
Ulomek zapišemo v obliki dveh števil, ki sta med seboj ločeni z vodoravno črto.
Zgornje število imenujemo števec, spodnje število pa imenovalec.
Imenovalec nam pove, na koliko enakih kosov je razdeljena celota. Števec pa nam pove, koliko takšnih kosov predstavlja naš del celote.
Ulomek je del celote, zato si ga najlažje predstavljamo z opazovanjem neke konkretne celote in njenih delov.
Pri tem si najpogosteje pomagamo z geometrijskimi liki, na primer s krogom ali s pravokotnikom.
Če želimo prikazati ulomek kot del lika:
lik najprej razdelimo na toliko enakih delov, kolikor znaša imenovalec ulomka ter
pobarvamo toliko delov, kolikor znaša števec ulomka.
Ulomek je pravzaprav drugačen zapis za deljenje. Predstavlja namreč deljenje števca z imenovalcem:

Spomnimo se, da deljenje z 0 ni definirano. Zato tudi ulomek z imenovalcem 0 nima pomena, saj celote ne moremo razdeliti na 0 delov.
Ulomek 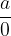 , pri čemer je a poljubno število, je nedefiniran in brez pomena.
, pri čemer je a poljubno število, je nedefiniran in brez pomena.
Glede na rezultat deljenja ločimo več vrst ulomkov. Ti se razlikujejo tako po velikosti kot po načinu zapisa.
Ko računamo vrednost ulomka, v katerem števec ni večkratnik imenovalca, potem se deljenje ne izide in dobimo decimalno število. Ulomek lahko v tem primeru zapišemo kot decimalno število.
Če je števec ulomka večkratnik imenovalca, se deljenje izide in ulomek lahko zapišemo v obliki naravnega števila.
Velja tudi obratno. Naravno število lahko zapišemo kot ulomek. To pa velja za vsako naravno število.
Najenostavnejši je tak ulomek, ki ima imenovalec 1. Takšen ulomek dobimo tako, da pod naravnim številom dopišemo ulomkovo črto in v imenovalec zapišemo 1.
Naravna števila običajno pretvarjamo v ulomke, ko imamo v računu naravna števila in ulomke.
Velja, da naravno število preoblikujemo v ulomek s poljubnim imenovalcem, le da imenovalec ni 0. Če naredimo takšno pretvorbo, moramo paziti, da ohranimo isto vrednost. To pomeni, če delimo števec in imenovalec ulomka, mora biti vrednost ulomka enaka naravnemu številu od prej.
Če je števec večkratnik imenovalca, lahko ulomek zapišemo kot naravno število.
Vsako naravno število n lahko zapišemo kot ulomek 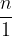 ali pa kot ulomek s poljubnim imenovalcem, ki ni enak 0.
ali pa kot ulomek s poljubnim imenovalcem, ki ni enak 0.
Če je števec ulomka enak imenovalcu, potem je ulomek enak 1.
Če je števec ulomka manjši od imenovalca, je rezultat deljenja manjši od 1. Tak ulomek imenujemo tudi pravi ulomek.
Vrednost ulomka, ki ima števec manjši od imenovalca, je manjša od 1.
Če je števec ulomka enak 0, je vrednost ulomka enaka 0. Imamo namreč 0 delov celote. Pri tem vrednost imenovalca ne sme biti enaka 0.
Ulomek  , pri čemer je a poljubno naravno število, je enak 0.
, pri čemer je a poljubno naravno število, je enak 0.
Če je števec ulomka večji od imenovalca, je rezultat deljenja večji od 1. Tak ulomek imenujemo tudi nepravi ulomek.
Vrednost ulomka, ki ima števec večji od imenovalca, je večja od 1.
Nepravi ulomek lahko zapišemo v obliki celega dela in ulomka, manjšega od 1. Tak zapis imenujemo tudi mešano število.
Naredimo lahko tudi obratno - mešano število zapišemo kot nepravi ulomek.
Ulomke lahko umestimo tudi na številsko premico. S tem vidimo, kako veliki so, oziroma kako daleč so od izhodišča. V postopku umeščanja ulomka na številsko os:
najprej upoštevamo njegov celi del in se premaknemo za toliko števil v desno,
zatem pa desno od tega števila upoštevamo še ulomkov neceli del, tako da ga prikažemo kot del celote do naslednjega naravnega števila.
Razširjanje ulomka je množenje števca in imenovalca z enakim številom, različnim od 0 in 1.
Če ulomek razširimo s številom 2, to pomeni, da celoto razrežemo na dvakrat več kosov. S tem se podvoji tako število v števcu kot v imenovalcu. Celota je torej razrezana na manjše kose, vendar jih imamo tudi mi več v števcu. Zato se vrednost ulomka nič ne spremeni.
Ulomek lahko razširimo na poljuben celoštevilski števec ali imenovalec, razen 0.
Ulomek razširimo tako, da tako števec in imenovalec množimo z istim številom, različnim od 0 in 1.
Vrednost ulomka se s tem ne spremeni.
Krajšanje ulomka je deljenje števca in imenovalca z enakim številom, različnim od 0 in 1. To je torej obratno od razširjanja ulomka.
Ulomek krajšamo tako, da tako števec in imenovalec delimo z istim številom, različnim od 0 in 1.
Pri tem se vrednost ulomka ne spremeni.
Ulomek lahko krajšamo večkrat, vse dokler števec in imenovalec nimata več nobenega skupnega delitelja razen števila 1. Ko se to zgodi, je ulomek okrajšan, števili v števcu in imenovalcu pa sta si tuji.
Ulomek najlažje krajšamo z malimi praštevili (2,3,5,7...). Z enim praštevilom lahko krajšamo večkrat, vrstni red krajšanja pa je poljuben.
Okrajšani ulomek ima v števcu in imenovalcu tuji si števili.
Okrajšani ulomek predstavlja enak delež kot prvotni ulomek.
Ulomek v enem koraku okrajšamo tako, da števec in imenovalec delimo z njunim največjim skupnim deliteljem.
Če ima več ulomkov enak števec ali imenovalec, jih lahko po velikosti primerjamo neposredno. Če pa niso enaki v števcih ali imenovalcih, jih bomo razširili na enak imenovalec.
Med ulomki z enakimi imenovalci je:
najmanjši tisti ulomek, ki ima najmanjši števec
največji pa je tisti, ki ima največji števec.
Med ulomki z enakimi števci je:
najmanjši ulomek tisti, ki ima največji imenovalec,
največji pa tisti, ki ima najmanjši imenovalec.
V primeru, da se ulomki razlikujejo tako po števcih kot po imenovalcih, bomo ulomke lahko primerjali šele potem, ko jih razširimo na skupni imenovalec.
Skupni imenovalec je lahko vsak skupni večkratnik števil v imenovalcih danih ulomkov. Običajno pa ulomke razširimo na najmanjši skupni imenovalec. To je najmanjši skupni večkratnik števil v imenovalcih danih ulomkov.
Ulomke lahko primerjamo po velikosti tudi tako, da jih najprej pretvorimo v decimalna števila. Vendar imamo s tem običajno več dela in možnosti za napako.
Desetiški ulomek ima v imenovalcu potenco števila 10, torej 10, 100, 1000, ...
Desetiški so tudi tisti ulomki, ki v imenovalcu nimajo potence števila 10, a jih lahko v tako obliko preoblikujemo bodisi s krajšanjem bodisi z razširjanjem.
Ker ulomkova črta predstavlja deljenje, števec delimo z imenovalcem in dobimo decimalno število.
Če je ulomek desetiški, ga lahko zapišemo v obliki končnega decimalnega števila. Tako število ima končno število decimalk, ki niso enake 0.
Če ulomek ni desetiški, pa se v količniku določen del decimalk periodično ponavlja v neskončnost. Tak zapis imenujemo periodično decimalno število, ponovljeno zaporedje števk pa perioda.
Takšna števila, pri katerih se ponavlja perioda, so najlepše zapisana z ulomkom.
Ulomke lahko seštevamo in odštevamo le, če imajo enak imenovalec. To pomeni, da lahko seštevamo ali odštevamo samo enako velike kose celote.
Polovic in tretjin ne moremo sešteti iz istega razloga, kot ne moremo sešteti jabolk in hrušk. Kosi niso enaki.
Ko seštevamo ulomke z enakimi imenovalci, ulomke najprej zapišemo na skupno ulomkovo črto.
To naredimo tako, da:
vse števce seštejemo nad ulomkovo črto,
skupni imenovalec vseh ulomkov pa zapišemo pod ulomkovo črto.
Tudi vsota ulomkov je ulomek. Preden zapišemo končni rezultat seštevanja, preverimo:
če je dobljen ulomek možno še okrajšati - v tem primeru ga moramo okrajšati
če ga lahko zapišemo v obliki mešanega števila - v tem primeru ga zapišemo z mešanim številom.
Mešano število je enako kot vsota celega in necelega dela ulomka. Pomeni namreč, da imamo celi del in dodatno še neceli del ulomka
Če je kateri izmed seštevancev mešano število, ga ni potrebno pretvarjati v nepravi ulomek, ampak lahko seštejemo posebej cele dele in posebej ulomke, manjše od 1.
Ulomke lahko seštejemo le, če imajo enake imenovalce. Pri tem ulomke zapišemo na skupno ulomkovo črto in seštejemo števca, imenovalec pa prepišemo.
Pri odštevanju ulomkov z enakimi imenovalci ulomka najprej zapišemo na skupno ulomkovo črto.
To naredimo tako, da:
števca odštejemo nad ulomkovo črto v istem vrstnem redu,
imenovalec pa prepišemo.
Če se imenovalci ulomkov razlikujejo, jih razširimo na najmanjši skupni imenovalec.
Tudi razlika ulomkov je ulomek. Preden zapišemo končni rezultat odštevanja, vedno preverimo, če je dobljen ulomek možno še okrajšati.
Ulomek lahko od celega števila odštejemo na več načinov:
celo število lahko takoj zapišemo kot ulomek,
ali pa prej celo število razdelimo na vsoto, da imamo manjše številke.
Pri odštevanju mešanega števila od mešanega števila je najlažje pretvoriti mešana števila v neprave ulomke in računati z njimi.
Ulomka lahko odštejemo le, če imata enake imenovalce. Pri tem ulomka zapišemo na skupno ulomkovo črto in odštejemo števca, imenovalec pa prepišemo.
Pri množenju in deljenju ulomkov se imenovalci lahko razlikujejo, pred začetkom računanja pa moramo vsa mešana števila zapisati kot neprave ulomke.
Pri množenju ulomka najprej zapišemo na skupno ulomkovo črto, nato pa zmnožimo:
števec prvega ulomka s števcem drugega ulomka in
imenovalec prvega ulomka z imenovalcem drugega ulomka.
Tudi produkt ulomkov je ulomek. Preden zapišemo končni rezultat množenja preverimo, če je dobljen ulomek možno še okrajšati ali zapisati v obliki mešanega števila.
Če v računu množenja nastopajo mešana števila, jih najprej zapišemo z nepravimi ulomki, cela števila pa kot ulomke z imenovalcem 1.
Pri množenju ulomke zapišemo na skupno ulomkovo črto, nato pa med seboj zmnožimo vse števce in vse imenovalce.
Na skupni ulomkovi črti lahko krajšamo poljuben faktor v števcu s poljubnim faktorjev v imenovalcu. To izhaja iz zakona o zamenjavi pri množenju. Zato je vseeno, če krajšamo števec enega ulomka z imenovalcem drugega ulomka.
Če po koncu krajšanja v imenovalcu ostane le še število 1, rezultat zapišemo v obliki naravnega števila.
Če imamo ulomek, v katerem v števcu in imenovalcu ni samih produktov, takrat števil ne smemo krajšati.
Najprej moramo izračunati vrednost števca in vrednost imenovalca, šele nato preverimo, če lahko ulomek okrajšamo.
Ulomke lahko krajšamo le takrat, ko so na ulomkovi črti samo produkti.
Poglejmo si pojem obratna vrednost ulomka.
Obratno vrednost ulomka dobimo tako, da zamenjamo mesti števca in imenovalca. Ulomek obrnemo okoli.
Zmnožek ulomka in njegove obratne vrednosti je enak 1.
Deljenje je obratna operacija od množenja. Zato lahko deljenje ulomkov zapišemo kot množenje
deljenca z
obratno vrednostjo delitelja.
Ulomka torej delimo tako, da deljenec zmnožimo z obratno vrednostjo delitelja.
Oglejmo si še nekaj primerov deljenja ulomkov.
Tudi količnik ulomkov je ulomek. Preden zapišemo končni rezultat množenja preverimo, če je dobljen ulomek možno še okrajšati ali zapisati v obliki mešanega števila.
Če v računu deljenja nastopajo mešana števila, pred postopkom le-ta zapišemo z nepravimi ulomki, cela števila pa kot ulomke z imenovalcem 1.
Ulomka delimo tako, da deljenec zmnožimo z obratno vrednostjo delitelja.
Rezultat seštevanja, odštevanja, množenja ali deljenja ulomkov mora biti okrajšan ulomek.