Osebne zbirke


Uporabo odvoda smo si v prejšnjem poglavju ogledali na polinomih in racionalnih funkcijah. V nadaljevanju si bomo pogledali še odvode nekaterih drugih funkcij.
Iz teorije vemo, da kompozitum funkcije lahko zapišemo kot:
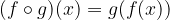
dobljeni rezultat pa imenujemo sestavljena funkcija, ki deluje tako, da se začetni element najprej preslika s funkcijo g, dobljeni element pa potem preslika še s funkcijo f.
Sedaj si poglejmo še odvod sestavljene funkcije. Vzamimo primer, ko imamo funkcijo, ki je ne znamo direktno odvajati. V tem primeru nam pride prav kompozitum, saj lahko dano funkcijo zapišemo kot sestavljeno funkcijo dveh funkcij, ki jih znamo odvajati. Poglejmo si pravilo za odvajanje kompozituma oziroma sestavljene funkcije:
Naj bo funkcija f odvedljiva v točki x, funkcija g pa odvedljiva v točki f(x). Potem je v točki x odvedljiva tudi sestavljena funkcija 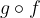 in velja:
in velja:
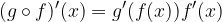
Naj bo dana korenska funkcija:
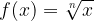
Odvajajmo jo:
Odvod korenske funkcije
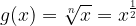
je enak
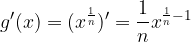
Na podoben način lahko poiščemo odvod funkcije 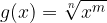 :
:
Odvod funkcije
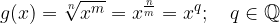
je enak
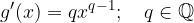
Najprej ponovimo, kaj je implicitna funkcija. Vemo, da je eksplicitno podana funkcija oblike
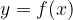
ki jo lahko zapišemo v implicitni obliki:
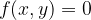
Do zdaj smo se že naučili odvajati eksplicitno zapisane funkcije. Včasih pa imamo podano funkcijo v implicitni obliki, ki je ni mogoče enostavno pretvoriti v eksplicitno obliko. Zato razmislimo, kako bi lahko odvajli funkcijo kar v implicitni obliki.
V osnovi se odvajanja implicitne funkcije lotimo tako:
Odvajamo obe strani enačbe.
Ker je y odvisen od x, y odvajamo kot posredno funkcijo.
Izrazimo odvod y'.