Osebne zbirke


Leče so optične naprave, ki izkoriščajo lom svetlobe. Pri vpadu svetlobe iz zraka na steklo ali katero drugo snov, kjer je hitrost širjenja svetlobe manjša od hitrosti v zraku (ali brezzračnem prostoru) se žarek lomi proti vpadnici - pravokotnici na mejno ploskev zrak - snov.
Slika predmeta, ki jo dobimo s pomočjo leče je lahko realna ali navidezna. V skicah bomo zato žarke, ki dajo realno sliko označevali s polno črto, navidezne žarke pa s prekinjeno črto. Kaj je realna in kaj je navidezna slika predmeta bomo spoznali na konkretnih primerih.
Za preslikavanje uporabljamo konveksne ali zbiralne leče in konkavne ali razpršilne leče. V nadaljevanju bomo smatrali, da so leče tanke, kar pomeni, da je debelina leče mnogo manjša od goriščne razdalje.
Zbiralna leča je lahko na sredini združen izsek dveh steklenih krogel. Na otip je izbočena, njena debelina na sredi je vedno večja od debeline na robovih - kar je shematsko predstavljeno na slikah 1 do 8.
Snop vzporednih svetlobnih žarkov, ki vpada na konveksno lečo pod določenim kotom, se na drugi strani združi v eno točko, ki leži na goriščni ravnini. Če so svetlobni žarki vzporedni z optično osjo, se na drugi strani združijo v gorišču.
Poglejmo sedaj nekaj pojmov in izrazov, ki jih uporabljamo pri vseh lečah (ne samo konveksnih) in so naznačeni na sliki 2.
Osnovni pojmi pri obravnavi leč:
Središče leče je točka na sredini leče in jo označimo z O.
Optična os je premica, ki gre skozi središče leče in je pravokotna na površino leče.
Gorišče leče F je točka, kjer se po odboju sekajo žarki, ki so pred odbojem vzporedni z optično osjo. Leča ima dve gorišči - levo in desno od središča leče.
Goriščna razdalja je oddaljenost gorišč od leče.
Goriščna ravnina je ravnina, ki jo prebada optična os pravokotno v točki gorišča. Na točki, ki leži na goriščni ravnini se združijo snopi vzporednih žarkov, ki vpadajo na lečo pod določenim kotom.
Konveksne leče uporabljamo za preslikave predmeta. Predmet velikosti P postavimo na neko razdaljo a pred lečo. Na razdalji b od leče dobimo sliko velikosti S. Slika je lahko pomanjšana, enako velika ali povečana glede na predmet. Lahko je pokončna ali obrnjena. Če ustvarjajo sliko realni žarki, je slika realna, če pa se sekajo navidezni žarki, je slika navidezna.
Žarki, predstavljeni na sliki 2, imajo enako poimenovanje pri konveksni in konkavni leči.
Poimenovanje žarkov v leči:
Osni žarek vpada v smeri optične osi in po prehodu skozi lečo nadaljuje pot po optični osi. Pri preslikavah vznožje predmeta P in slike S položimo na optično os in ga zrcalimo kot osni žarek.
Sredinski žarek je žarek, ki vpada na središče leče pod določenim kotom in po prehodu skozi lečo ohrani smer.
Žarek, ki je vzporeden z optično osjo (vzporedni žarek) gre na drugi strani leče skozi gorišče.
Goriščni žarek gre skozi gorišče na isti strani leče, kot je predmet in je po prehodu skozi lečo vzporeden z optično osjo.
Če pogledamo sliko 2, je slika S predmeta P realna (sekajo se realni žarki), pomanjšana in obrnjena.
Enačbi leče povezujeta velikost slike in predmeta, njuni oddaljenosti od leče in goriščno razdaljo. Enačbi konveksne leče (ki pa veljata tudi za konkavno lečo) dobimo z opazovanjem podobnih trikotnikov na sliki 3:
Najprej opazujmo vijolično šrafirana trikotnika. Vidimo, da je sta velikost predmeta in slike v istem razmerju, kot sta njuni razdalji od temena leče:

pri tem je P velikost predmeta, S pa velikost slike.
Opazujmo sedaj s poševimi črtami šrafirana podobna trikotnika. Dobimo:
Enačbi leče sta:
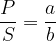
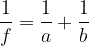
kjer je P velikost predmeta, S velikost slike, a oddaljenost predmeta od leče, b oddaljenost slike od leče in f goriščna razdalja.
Pri obrnjeni sliki smo vzeli pozitiven S; če bo slika pokončna bo zato S negativen.
Razdalji b in f sta lahko pozitivni ali negativni. Negativna razdalja je vedno razdalja navideznega žarka (glej primer na sliki 8) ali navideznega gorišča, kar bomo ilustrirali pri razpršilni leči (slika 9).
Kako se bo predmet preslikal s pomočjo konveksne leče, je odvisno od relativne oddaljenosti predmeta glede na goriščno razdaljo, kar kažejo naslednji primeri:
Slika je realna, pomanjšana in obrnjena.
Slika je realna, enako velika kot predmet in obrnjena
Slika je realna, povečana in obrnjena
Žarki na drugi strni leče so vzporedni, navidezni žarki tvorijo navidezno sliko v neskončnosti. Primer uporabe: lupa (povečevalno steklo)
Realni žarki se na drugi strani leče razpršijo. Na isti strani, kot je predmet se sekajo navidezni žarki in tvorijo navidezno sliko. Slika je povečana in pokončna.
V tem primeru je goriščna razdalja še vedno pozitivna, Pri izračunu razdalje predmeta bomo dobili negativen b, negativna (pokončna) bo tudi slika S.
Konkavna leča je sestavljena iz dveh krogelnih izsekov, kjer uporabimo notranji, konkavni del krogelne kapice. Na otip je leča vbočena, njena debelina na sredi je manjša od debeline na robovih. Shematsko je prikazana na sliki 9.
Pri konkavni leči se žarki po prehodu skozi lečo razpršijo. Realni žarki se ne bodo nikoli sekali. Sekajo pa se navidezni žarki, ki jih prikažemo kot podaljšek realnih žarkov na strani predmeta - slika 9. Označimo jih s prekinjeno črto. Slika je zato navidezna. Iz slike 9 tudi razberemo, da je slika predmeta pokončna in pomanjšana.
Veljata še vedno enačbi leče, ki smo ju izpeljali pri konveksni leči, že v podatkih pa moramo upoštevati, da je goriščna razdalja f negativna. Kot rezultat izračuna (glej primer) bomo videli, da bosta negativni tudi b in S.
Slika se nahaja na isti strani kot predmet. Oddaljenost slike od leče je vedno manjša od oddaljenosti predmeta od leče. Ker sta obe oddaljenosti v istem razmerju kot sta velikost slike in predmeta (glej enačba leče) sledi, da je tudi slika manjša od predmeta.
Slika je pri konkavni leči vedno navidezna, saj se realni žarki na drugi strani leče razpršijo. Slika je pokončna, goriščna razdalja in razdalja slike od leče pa sta negativni.
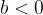
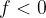
Absolutna vrednost oddaljenosti slike od leče b je vedno manjša od oddaljenosti predmeta a:
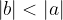
Sledi, da je tudi velikost slike vedno manjša od velikosti predmeta, saj velja enačba:
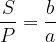
Leče lahko nizamo drugo za drugo tako, da dobimo sestavljene leče. Pri tem lahko sestavljamo konveksne leče (f>0), konkavne leče (f<0) ali pa kombinacije obeh. Predpostavimo, da so leče tanke in blizu skupaj.
Kot primer vzemimo dve konveksni leči, kot je narisano na sliki 10. Na goriščno razdaljo prve leče postavimo točkasto svetilo. Žarki, ki izhajajo iz gorišča prve leče, kjer je svetilo P dajo po lomu na prvi leči med obema lečama vzporedni snop svetlobe. Po lomu na drugi leči se žarki združijo v gorišču druge leče, kjer dobimo sliko svetila S.
Velja enačba leče:
Dobili smo goriščno razdaljo kombinacije dveh konveksnih leč.
Pri sestavljenih lečah velja, da se recipročne vrednosti goriščnih razdalj seštevajo:
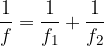
Recipročna vrednost goriščne razdalje se imenuje tudi dioptrija, zato lahko rečemo, da se pri nizanju leč dioptrije seštevajo.
Pojem dioptrije uporabljajo optiki za konstrukcijo leč. Dioptrija leče je odvisna od radija krogelnih kapic, iz katerih je sestavljena leča, lomnega količnika snovi in debeline leče; več o dioptriji lahko preberete v gradivu Dioptrija.
Dioptrija, ki jo označimo s črko D, je z goriščno razdaljo preprosto povezana:
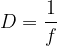
Če imamo več leč, ki so postavljene druga za drugo, smo v prejšnjem poglavju ugotovili, da se seštevajo recipročne vrednosti goriščnih razdalj:
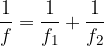
oziroma, če enačbo zapišemo z dioptrijo, se pri sestavljanju leč posamezne dioptrije med seboj seštevajo:
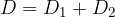
Primeri sestavljenih leč so očala, objektivi fotoaparatov itd, kar je podrobneje opisano v gradivu Optične naprave.