Osebne zbirke


Svetloba je elektromagnetno valovanja, enako kot so npr. radijski valovi. Lastnosti svetlobe so:
določa jo svetlobni tok ali svetlobna moč P[W].
hitrost svetlobnih valov c v brezzračnem prostoru je
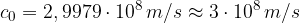
Če prodre svetloba v snov (steklo, voda itd.) se njena hitrost zmanjša.
frekvenca in valovna dolžina sta povezani prek enačbe:
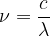
Frekvenca oziroma valovna dolžina določata barvo vidne svetlobe. Svetloba večje ali manjše valovne dolžine od vidne svetlobe se imenuje infrardeča svetloba in ultravioličasta svetloba:
Izvir svetlobe lahko oddaja svetlobo ene same valovne dolžine (pravimo ji monokromatska svetloba). Primer monokromatske svetlobe je svetloba laserja. Izvir lahko seva tudi več valovnih dolžin hkrati (pravimo, da seva svetlobni spekter). Primer je sonce, ki seva vse valovne dolžine vidne svetlobe (zvezni spekter).
Izvir svetlobe je lahko točkasto svetilo, ki seva svetlobo v vse smeri enako, ali pa je to svetilo, ki seva svetlobo samo v določeni smeri (npr. reflektor z odbojnim krogelnim ali parabolnim zrcalom, ki usmerja žarke samo v eno smer).
Podobno kot pri valovanju na kapljevini se tudi svetloba širi v smeri valovnih žarkov, ki se imenujejo svetlobni žarki. Če je svetilo zelo majhno (točkasto svetilo), se širi svetloba od izvira svetlobe radialno v vse smeri. Če pa so žarki vzporedni, tvorijo svetlobni snop. Svetlobni snop torej omejuje svetlobne žarke:
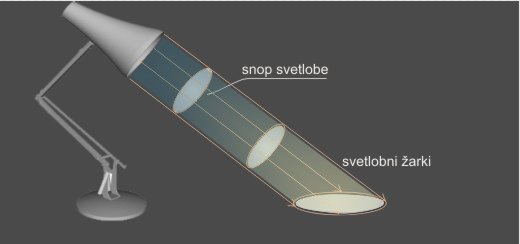
Slika 2: svetlobni žarki (puščice) in svetlobni snop svetila (v tem primeru elipsast lik) z usmerjeno svetlobo.
Kot smo uvodoma že povedali, se hitrost potovanja svetlobe v različnih snoveh razlikuje. Vzemimo svetlobo, ki prehaja pod določenim kotom iz snovi z višjo hitrostjo v snov z nižjo hitrostjo svetlobe. Pravimo tudi, da prehaja žarek iz optično redkejše snovi (kjer je hitrost svetlobe c večja) v optično gostejšo snov (kjer je hitrost svetlobe c manjša). Na sliki 3 so izrisani grebeni vala, ki smo jih srečali tudi pri valovanju na kapljevini. Sedaj jih imenujmo svetlobne valovne fronte. Razdalja med dvema valovnima frontama je valovna dolžina (glej sliko 3).
Opazujemo lahko več svetlobnih pojavov. Svetloba se delno odbije, delno pa prodre v drugo snov, obenem pa se ji zmanjša valovna dolžina in na mejni ploskvi se lomi:
Del svetlobe se na mejni ploskvi odbije. Velja lomni zakon. Ta pravi, da je pri vpadu svetlobe na gladko ploskev vpadni kot 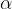 enak odbitemu. Vpadni kot merimo od navpičnice na mejno ploskev, enako tudi odbojni kot (glej kot
enak odbitemu. Vpadni kot merimo od navpičnice na mejno ploskev, enako tudi odbojni kot (glej kot 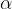 na sliki 3).
na sliki 3).
Pri odboju svetlobe vedno predpostavimo, da je hrapavost mejne površine veliko manjša od valovne dolžine. V nasprotnem primeru se odbiti žarek razprši.
Pri odboju svetlobe na gladki povrišini se svetloba odbije tako, da je vpadni kot 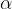 enak odbojnemu kotu.
enak odbojnemu kotu.
Pri prehodu iz optično redkejše v optično gostejšo snov se valovne fronte stisnejo. Ker je razdalja med dvema valovnima frontama enaka valovni dolžini, pomeni, da se je valovna dolžina zmanjšala. Zakaj?
Izhajamo iz enakosti frekvenc v obeh snoveh. Zato velja enačba:
Če prehaja svetloba iz optično redkejše v optično gostejšo snov ali obratno. se spremeni valovna dolžina. Valovni dolžini v obeh snoveh sta v istem razmerju kot hitrosti svetlobe v obeh snoveh in sicer:
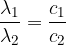
Svetloba se tudi lomi. To pomeni, da vpadni kot ni enak lomnemu kotu. Val izbere tisto pot, za katero porabi najmanj časa. To je Fermatov zakon. Izpeljava tega zakona je precej zahtevna, zato bomo lomni zakon izpeljali na bolj preprost način.
Vzemimo primer, ko vpada svetloba pod določenim kotom v snov, kjer se njena hitrost zmanjša glede na hitrost vpadnega žarka.
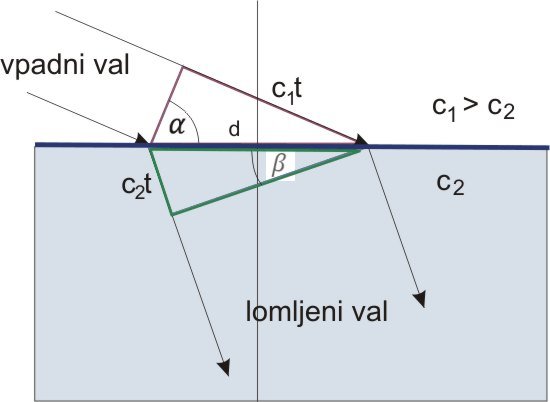
Slika 4: lom svetlobe; pri tem bodimo pozorni na kota 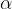 in
in 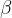 , ki, čeprav malce drugače naznačena, sta še vedno kota, ki določata odklon žarka od navpičnice na mejno ploskev.
, ki, čeprav malce drugače naznačena, sta še vedno kota, ki določata odklon žarka od navpičnice na mejno ploskev.
Vpadni val vpada pod kotom 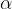 glede na navpičnico na mejno ploskev dveh snovi. V prvi snovi je hitrost valovanja
glede na navpičnico na mejno ploskev dveh snovi. V prvi snovi je hitrost valovanja 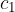 , v drugi pa
, v drugi pa 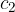 (glej sliko 4). Naj bo:
(glej sliko 4). Naj bo:
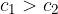
Na stični ploskvi prepotuje val v času t daljšo razdaljo (saj je hitrost večja) 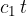 kot v drugi ploskve, ko naredi v istem času razdaljo
kot v drugi ploskve, ko naredi v istem času razdaljo 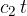 . Na sliki 4 sta na zgornji in spodnji polovici mejne ploskve označena dva pravokotna trikotnika.
. Na sliki 4 sta na zgornji in spodnji polovici mejne ploskve označena dva pravokotna trikotnika.
Poglejmo zgornji, vijolično obrobljen trikotnik. Velja:
In še spodnji, zeleno obrobljen trikotnik:
Izenačimo razdaljo d v zgornjih enačbah in dobimo:
V kolikor je zgornja snov v sliki 2 zrak ali vakuum, lahko zapišemo:
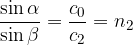
Pri tem je 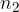 lomni količnik druge snovi.
lomni količnik druge snovi.
Lomni količnik nam pove, kolikokrat hitreje potuje svetloba v brezzračnem prostoru kot v opazovani snovi.
Preoblikujemo sedaj enačbo (1). V ta namen množimo števec in imenovalec desne strani enačbe s 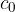 :
:
Enačbi (1) in (2) sta dve obliki lomnega zakona.
Žarek, ki pade poševno na mejno ploskev se delno odbije, delno pa pronica v snov. Del žarka, ki se odbije, se odbije pod istim kotom, glede na navpičnico, pod kakršnim je vpadel.
Del žarka, ki pa pronica v snov, pa pronica pod takim kotom 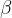 , da velja:
, da velja:
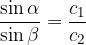
kjer je 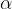 kot, pod katerim je žarek vpadel,
kot, pod katerim je žarek vpadel, 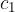 in
in 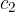 pa hitrosti potovanja svetlobe v prvi in drugi snovi.
pa hitrosti potovanja svetlobe v prvi in drugi snovi.
Lomna količnika za prvo in drugo snov sta:
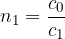
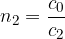
Lomni zakon lahko zapišemo tudi v obliki:
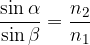
Iz lomnega zakona lahko ugotovimo, da če žarek prehaja v optično gostejšo snov (kjer je hitrost c manjša), se lomi k navpičnici, če prehaja v optično rekejšo snov (kjer je hitrost c večja) pa stran od navpičnice. Poglejmo lomne količnike za nekatere snovi:
Predpostavimo, da prehaja svetloba iz snovi z nižjo hitrostjo širjenja v snov z višjo hitrost širjenja npr. iz vode v zrak. Tudi v tem primeru velja slika 4, le da obrnemo smer žarka:
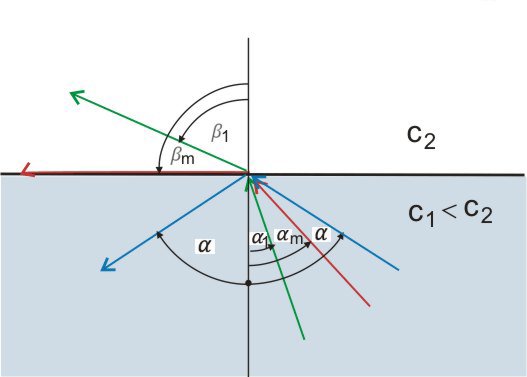
Slika 5: lom v optično redkejše sredstvo (zeleni žarek), mejni primer (rdeč žarek) in popolni odboj (modri žarek).
Lomni kot je sedaj večji od vpadnega (zeleni žarek na sliki 5). Poečajmo vpadni kot 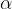 tako, da postane lomni kot natanko 90 stopinj. Dobili smo mejni kot totalnega odboja (glej rdeče obarvan žarek na sliki 5).
tako, da postane lomni kot natanko 90 stopinj. Dobili smo mejni kot totalnega odboja (glej rdeče obarvan žarek na sliki 5).
Poiščimo kot popolnega odboja oziroma mejni kot 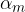 :
:
Dobili smo sinus mejnega kota, pri katerem pride do totalnega odboja (slika 5, rdeči žarek). Če še povečamo vpadni kot, se svetlobni žarek na mejni površini odbije, in ne prehaja več v optično redkejše snov (glej modri žarek na sliki 5). Tedaj velja zakon odboja: vpadni in odbojni kot 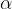 sta enaka.
sta enaka.
Do popolnega odboja pride, če se žarek širi iz optično gostejše snovi proti optično redkejši snovi. Če je vpadni kot dovolj velik, tako, da velja:
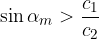
ali:
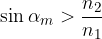
se žarek popolnoma odbije od mejne površine in ne prodre več v drugo snov. Tedaj velja lomni zakon za odbiti
žarek: vpadni kot je enak odbojnemu kotu.