Prijava z e-naslovom
Prijava brez gesla
Kristal je v fiziki in kemiji izraz za snov, ki ima geometrijsko pravilno razporeditev gradnikov. In kristalografija je področje naravoslovja, ki proučuje zgradbo kristalov.
Ta urejenost se včasih (ne pa vedno) odraža tudi navzven, v npr. ravnih robovih in ploskvah snovi.
Če so nas v gradivu Lastnosti trdnih snovi zanimale lastnosti snovi, ki so posledica:
tipov gradnikov (kateri atom, ion, molekula sestavlja snov) in
vezi med njimi,
nas bodo v tem gradivu zanimali kristali s stališča razporeditve gradnikov v prostoru. Pri tem ne bo pomembno, kateri gradniki (atomi, ioni ali molekule) sestavljajo snov. Kristalografski opis je neodvisen od tipa gradnikov in vezi med njimi in ne govori o lastnostih, le o obliki kristalov.
Urejena razporeditev gradnikov pomeni, da:
se gradniki snovi v prostoru ponavljajo
v enakomernih razmakih.
Kot rečeno, tip gradnikov ne določa njihove razporeditve v prostoru. Zato lahko opisovanje strukture poenostavimo tako, da gradnike "zamenjamo" s točkami v prostoru. Te točke tvorijo namišljeno mrežo, ki jo imenujemo kristalna mreža:
Osnovna celica je del kristala, ki se v prostoru ponavlja. Celoten kristal neke snovi sestavimo tako, da "zlagamo skupaj" osnovne celice.
Osnovna celica je vedno paralelepiped, to je geometrijsko telo s tremi pari vzporednih ploskev oziroma pokončna ali poševna štiristrana prizma. Kristalno strukturo opišemo s tem, ko opišemo osnovno celico. Pri tem moramo navesti:
dimenzije osnovne celice
Osnovna celica je določena z naslednjimi dimenzijami (pravimo jim tudi konstante):
dolžinami svojih robov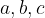 
in
koti med njimi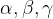 
.
tip osnovne celice
Tip osnovne celice določa lego oziroma razporeditev gradnikov v osnovni celici. Tipe osnovnih celic podrobneje spoznamo v nadaljevanju.
Glede na dimenzije in obliko osnovnih celic razlikujemo šest kristalnih razredov (rečemo tudi kristalnih sistemov, singonij). Naštejmo jih.
Tabela 1: Kristalni razredi (singonije)
Gradniki se vedno nahajajo v:
vseh ogliščih osnovne celice,
lahko pa tudi v sredini ali na stranskih ploskvah osnovne celice.
Poznamo štiri možne razporeditve gradnikov oziroma štiri tipe osnovnih celic. Tukaj obravnavamo le enostavne kristalne strukture, ki spadajo v prve tri tipe.
Tabela 2: tipi osnovnih celic:
V tabeli 2 so navedeni primeri za kubični kristalni razred. Različni tipi osnovnih celic se sicer lahko pojavijo tudi v drugih kristalnih razredih. V praksi pa se sicer ne pojavijo vsi tipi v vseh razredih, vse kombinacije niso možne.
V resničnem kristalu je "zloženih skupaj" veliko število osnovnih celic. Realni gradniki kristala pa niso točke, ampak imajo neko svojo velikost. Zato gradniki v ogliščih in na ploskvah osnovne celice v resnici segajo v več osnovnih celic.
Če želimo izračunati število gradnikov znotraj ene osnovne celice, upoštevamo pravila, ki veljajo za gradnike na:
ogliščih,
ploskvah,
centru celic.
Poglejmo si pravila za vsako lego gradnika posebej. Gradnike za boljšo predstavo povečajmo v večje krogle.
Gradnik v oglišču
Gradnik, ki je v oglišču osnovne celice, pripada osmim osnovnim celicam:
Gradnik v oglišču osnovne celice.
Znotraj določene osnovne celice je zato le 1/8 tega gradnika.
Gradnik na mejni ploskvi
Gradnik na ploskvi pripada dvema osnovnima celicema:
Gradnik na ploskvi osnovne celice.
Znotraj ene osnovne celice je zato le 1/2 gradnika.
Gradnik v sredini telesno centrirane osnovne celice
Ker je gradnik v celoti znotraj ene same celice, v celoti pripada dani osnovni celici.
Gradnik v sredini osnovne celice.
Koordinacijsko število pove, s koliko atomi (ali atomskimi skupinami - ioni, molekulami) je obdan nek izbrani atom.
Pri kovinskih in kovalentnih kristalih, ki vsebujejo le eno vrsto atomov, navedemo le eno koordinacijsko število.
V ionskih kristalih navedemo dve koordinacijski števili in sicer v naslednjem vrstnem redu:
število anionov okrog kationa in
število kationov okrog aniona.
Za molekulske kristale in kompleksnejše ionske kristale (ki vsebujejo sestavljene ione) običajno ne navajamo koordinacijskega števila.
Kot smo že spoznali, pri ionskih kristalih navajamo dve koordinacijski števili, saj ti kristali vsebujejo dve vrsti gradnikov. Ta zapis bomo ponovno pojasnili na primeru kristala NaCl, ki ga zdaj že dobro poznamo.
